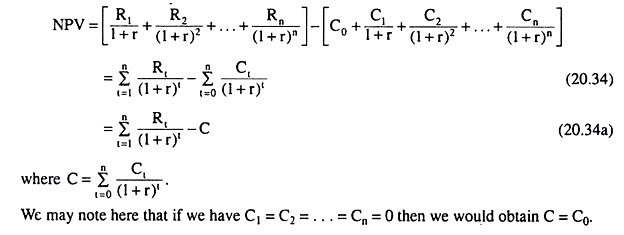Top 4 Methods of Project Evaluation | Firm

The following points highlight the top four methods of project evaluation in a firm. The methods are: 1. Return of Investment (ROI) 2. Payback Method 3. Net Present Value (NPV) 4. The Internal Rate of Return (IRR).

Method # 1. Return of Investment (ROI):

The ratio of profit expected from an investment project and the proposed investment for the project is called Return on Investment (ROI).

So we may write:

This ROI ratio is used as a criterion for the evaluation of an investment project. The greater the ROI of a project, the greater is its acceptability. There are three concepts about the amount of investment on a project. The amount of investment may mean the amount of assets, amount of capital invested, or the amount of equity capital. We may obtain three types of ROI on the basis of these three concepts.

These are:

(i) Return on Assets (ROA):

By definition, ROA is the ratio between net profit and the assets. We may write, therefore,

Here net profit does not include the interest to be paid to the lenders. But, since interest is included in the real return on total assets, an improved form of ROA is

(ii) Return on Capital Employed (ROCE):

ROCE is the second type of ROI. Here net profit, excluding tax, is expressed as a ratio of the total amount of invested capital. The total amount of capital provided by the owner of the firm and the lenders is the total invested capital in this case.

We may have this estimate of capital in two ways.

First, the total amount of invested capital is the sum total of long-term liabilities and equity of the shareholders.

Second, invested capital is the summation of the net circulating capital and fixed assets.

Therefore, we may write here

Again, we may include the interest paid in net profit and write

(iii) Return on Shareholders’ Equity (ROSE):

By definition, a general estimate of ROSE is

Now the shares of a company may be of two types: preference shares and ordinary shares. Here, if the shares are ordinary shares, then we may write

We may mention here two more measures of the rate at which the owners of ordinary shares may obtain return from their company. These two rates of return are “earning per share” (EPS) and “dividend per share” (DPS).

By definition, we have

It may be noted here that the share owners may earn at the rate of EPS only when the company actually distributes all the money equal to the numerator of the formula for EPS among the shareholders.

Method # 2. Payback Method:

If an investment project is implemented, then the time or the number of years within which the summation of the flow of undiscounted net revenues becomes equal to the total cost of the project is called the payback period.

According to this method, if one of a number of projects is to be selected, then the project for which the payback period is minimum, should be implemented.

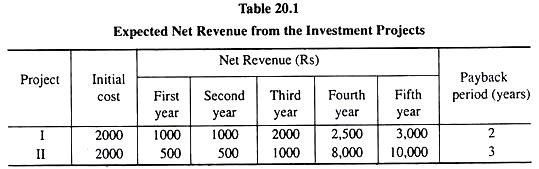
To illustrate the point let us take help of an example. Let us suppose that the expected flows of net revenue from two different projects and the costs of these projects are given in the table below.

From the data given above we see that in the case of project I, the sum total of the net revenue flow in the first two years has been equal to the project cost and, in the case of project II, the sum total of the net revenue flow in the first three years has been equal to the project cost.

In other words, the payback period for the two projects are 2 and 3 years, respectively. According to the payback method, if one of the two projects are to be implemented then the project I should be selected for implementation, for the payback period of this project is shorter than project II.

Limitations:

Payback method is not very suitable for evaluation of investment projects. This is be­cause, as we see in the above example, that it is project II—not project I—that is more profitable to the firm. For, in the fourth and fifth years, the flow of net revenue from project II is much more than that from project I.

In fact, if we use any acceptable discount rate to estimate the present value of the revenue flows of the two projects, we would see that the present value of project II is greater than that of project I. Therefore, implementation of project II is more profitable for the firm than that of project I.

Yet the payback method would prescribe the implementation of project I. Actually, the payback method may quite often lead the firm to take a wrong decision, because the method does not consider the expected rev­enues of all the years.

Method # 3. Net Present Value (NPV):

Definition of NPV:

Let us suppose that from some investment project the firm expects to obtain net revenues of R] in the 1st year, R₂ in the 2nd year,…, R_n in the nth year. Let us also suppose that the initial cost of the project is C₀ and apart from this, the firm would have to spend on the project an amount of Q in the 1st year, C₂ in the second year,…, C_n in the nth year.

If we now deduct the present value of the flow of costs of the project from the present value of the flow of net revenues, we would obtain the net present value (NPV) of the project.

In order to obtain the present values of the flows of revenue and cost, we shall use the rate of cost of capital (r) as the discount rate, and we shall assume that the revenue of a particular year would be obtained at the end of the year, and cost of any year should also be paid at the end of the year. Therefore, by definition, we obtain the net present value (NPV) for the project to be

Accept-Reject Rule:

It follows from the definition of NPV, or, from equations (20.34) or (20.34a) that, if for an investment project, we have NPV > 0, then the revenue from the project is greater than its cost, i.e., the project is profitable, and, if the firm accepts the project, then the value of the firm would increase. In other words, if NPV > 0, the project would be accepted.

On the other hand, if NPV < 0, the cost of project would be greater than its revenue, and so, if the project is accepted the firm would have to suffer-a loss and its value would decrease. Therefore, if NPV < 0, the project would be rejected.

Lastly, if NPV = 0, the revenue and cost of the project would be equal. In this case, the firm would be neutral or indifferent between the acceptance and rejection of the project.

Now, let us suppose that there are n acceptable (NPV > 0) projects and the firm would have to select k number of them (k < n). In this case, the firm would have to arrange the projects in the descending order of their NPVs and should select the first k number of the projects.

Evaluation of the NPV Method:

We have discussed above the properties of a good project evaluation method. The NPV method has all these properties. Therefore, it is a good project evaluation method.

The good properties of the NPV method are:

(i) The method uses the rate of opportunity cost of capital as the discount rate in order to find the present value of all expected revenues and costs.

(ii) The method considers all the expected flows of revenues and costs of the concerned investment project.

(iii) If k number of profitable investment projects are to be selected from n such projects (k < n), then the NPV method arranges all the n number of projects in the descending order of their NPVs and selects the first k number of projects out of this arrangement, for implementa­tion. As a result, the firm’s value is maximised.

(iv) The NPV method separately evaluates each particular project (independent of any alter­native project).

Although the NPV method possesses the above good properties, it has some disadvantages also. These are:

(i) Here the task of estimating the present value of revenues and costs is fairly complex, although it is not impossible.

(ii) Here the rate of cost of capital has been taken as the discount rate. But the cost of different types of capital may be different and the method of estimation of the cost of capital is not at all simple.

(iii) In the NPV method, of the two different investment projects, one with a higher NPV is selected for implementation. But the project with a higher NPV may very well be the project with a higher initial investment. This the method does not consider. That is why many people do not consider this method as a dependable one.

(iv) Lastly, the project with a higher NPV may have a higher life and for that reason it may be less acceptable. But according to the NPV method, a project should be selected only if the NPV is higher. That is, the method does not think that the life of the project should also be considered while determining its acceptability. That is why the method is not considered to be a dependable method.

Method # 4. The Internal Rate of Return (IRR):

Definition of IRR:

The Internal Rate of Return (IRR) is a rate of discount (m) that makes the present value of the expected revenues to be obtained from an investment project equal to the present value of the cost of the project.

Let us suppose that from an investment project with n years of life, the expected revenues to be obtained at the end of years 1,2………………. n are, respectively, R₁, R₂, . . ., R_n. Let us also suppose that the initial cost of the project is C₀ and the costs to be incurred at the end of different years are C₁, C₂,..C_n. Therefore, here the present value (PV) of the costs of the project would be

Here m is such a rate of discount that would make the sum total of the present values of R₁, R₂,…., R_n, equal to C. Therefore, by definition, m is the internal rate of return of the project. This IRR has been called by Keynes the marginal efficiency of capital.

We may easily understand why m is called the IRR. For the implementation of the project, the firm spends at present a sum of money equal to C. In equation (20.37), we see that spending a sum of money equal to C means simultaneous spending of the sums R₁/1 + m, R₂/(1+m)² …. R_n/(1+m)ⁿ.

Now, the firm spends R₁/1+m of money at present and it (expectedly) recovers R₁ of money at the end of the first year—here the rate of return is m which is equal to the rate of discount.

Again, the firm spends R₂/(1+m)² of money at present and it recovers R₂ of money at the end of the second year, the rate of return being again m. Proceeding in this way, ultimately we see that the firm spends R_n/(1+m)ⁿ of money at present and recovers R_n of money at the end of the nth year, the rate of return being again m.

Therefore, what we have seen is that the firm spends at present an amount of money C on the project and earns a rate of return m on each and every portion of this investment. That is why m is called the internal rate of return or average rate of return.

Accept-Reject Rule:

If the IRR is greater than the rate of cost of capital, then investment in the concerned project would be profitable. That is, if the rate of cost of capital is r, then the project should be imple­mented if m > r.

On the other hand, if m < r, then the project would not be profitable—if it is taken up for implementation, then the value of the firm would decrease. Lastly, if m = r, then the firm would be neutral between accepting and rejecting the project, for the firm’s value would remain unchanged even if the project is implemented.

Evaluation of the IRR Method:

The IRR method takes into consideration almost all the things that should be considered for the evaluation of an investment project. Therefore, the method is accepted as a good method.

We can present the following points in favour of this method:

(i) The IRR method determines the rate of return on the basis of the present values of all the expected revenue and cost figures. That is, the time-value of money is considered in this method.

(ii) The IRR method considers all the revenue and cost flows that may be obtained in an investment project.

(iii) If only a few projects are to be selected out of a number of mutually exclusive and profitable [IRR (= m) > r] projects, then all these projects are arranged in the descending order of their IRRs and then the required number of projects from the beginning of this arrangement are taken up for implementation. As a consequence, the firm’s value increases to the maximum possible extent.

(iv) The IRR method evaluates each project separately, i.e., independently of any alterna­tive project. However, the IRR method has certain disadvantages. These are:

(i) If the firm has to incur costs for the project in different years, apart from the initial costs, then the present values of these costs would have to be calculated, which is not an easy task. Besides, the rate of cost of capital which is used as the rate of discount here, is also not easy to determine.

(ii) Another drawback of the method is that if the life of the project is more than three years (n > 3), then to find the value of m by solving equation (20.37) is also a complicated job. If n > 3, then the value of m has to be obtained by a trial and error method.

(iii) If one of a number of different projects is to be selected for implementation by the IRR method, then the project with the highest IRR has to be selected. But, in practice, this project may not be maximum profitable or it may not succeed in maximising the wealth of the share­holders of the firm.

(iv) Lastly, it is assumed in the IRR method that the flow of cash obtained from a project is reinvested at a rate which is equal to IRR = m. For example, if two projects have IRRs of 16 per cent and 20 per cent, respectively, then it is assumed that the cash flows from the projects should be reinvested at the rates of 16 per cent and 20 per cent, respectively. But it is not at all realistic to assume that a firm can Reinvest its cash flows at two different rates.