Role of Government in a Modern Economy

In this article we will discuss about the Role of Government in a Modern Economy.

The government plays a very important role in a modern economy. Of course, there is contro­versy among economists regarding the optimal level of government intervention in the economy. How­ever, the fact remains that government expenditure and taxation programmes exert considerable influ­ence on national income, output and other key macro-economic variables.

Our analysis of national income determination so far has concentrated on the private sector of the economy. The picture that emerges is one of a fluctuating economy in which it is difficult, if not im­possible, to achieve stability. This means that a free- enterprise (or uncontrolled) economy will be charac­terized by unemployment, business failures, insecu­rity, loss of potential output, or even inflation.

As a result modern nations have turned to governments to promote greater economic stability.However, it is not that easy to achieve a stable, full-employment economy. The economy is not static. Instead its capacity to produce increases continuously. So the policies that bring full employment this year may be grossly inadequate next year.

Moreover, there is often a conflict between full employment and price level stability. The government planners and policy­makers have to make difficult but pragmatic compro­mises between the two social evils: unemployment and inflation.

The government seeks to promote full employ­ment and price stability through its power to tax and spend, which comprise what is called fiscal policy, it refers to taxation and spending on the part of the gov­ernment.

These are shown in the budget, whose size and balance (or imbalance) clearly indicate how much influence the government is likely (able) to exert on aggregate effective demand. It was J.M. Keynes who first pointed out that the government budget can be manipulated as to increase or decrease aggregate de­mand and, through it, influence the level of employ­ment and output as well as the incomes of the pro­ducers.

Two basic principles underlying fiscal policy are the following:

1. Taxes reduce aggregate demand by reducing disposable income of the community.

2. Government expenditure on goods and ser­vices produced in the private sector add to aggregate demand by channelling purchasing power back into the flow of spending.

It logically follows from these two basic princi­ples that economic activity can be slowed down by raising taxes and/or reducing government expendi­tures. These fiscal actions reduce the flow of real spending in the economy. They are considered to be appropriate when the economy is threatened by inflation of demand-pull variety.

On the other hand an exactly opposite type of fiscal action is called for when the economy is in deep depression. So the gov­ernment has to reduce taxes and/or increase its own spending. These will have the effect of increasing the flow of spending and enlarging aggregate demand. Such measures become absolutely essential when un­employment threatens to increase and the economy needs a stimulus.

These basic propositions have to be borne in mind when discussing the role of government in the circular flow of income. We may now integrate these propo­sitions into the general analysis of national income determination.

Government and the Determination of the National Income (Product):

When we consider government spending a new factor is added to the determinants of aggregate de­mand. Government purchases of goods and services will now add to consumption and investment spend­ing in determining the level of national product and income.

So the basic equation, which expresses the equilibrium condition of national income becomes:

E = C + I + G

where G is government purchases of goods and ser­vices.

However, to cover its ever-growing expenditure, the government has to collect revenue from different sources. The most important source is tax. Thus a portion of national income is taxed away by the gov­ernment.

As a result the equation for the uses of the national income becomes:

Y = C + S + T

where T stands for taxes paid to the government. Here we ignore indirect taxes as also corporate taxes. So T stands for income taxes imposed on households. Such taxes reduce the disposable income of the peo­ple, as the following example will show.

Problem 1:

Assume that consumption is a linear function of ‘disposable’ income and realised taxes are a linear function of realised national income. With exogenously given government expenditure and pri­vate investment how can you establish a relationship between a change in the tax rate and a change in na­tional income?

Solution:

From the above assumptions we can build up three equations:

C = a + b(Y — T)

T = t. Y

Y = C + I + G

(i) Consumption function

(ii) Tax function

(iii) Income equation

where Y. C. I. G. t stand respectively for national in­come, consumption, private investment, government expenditure, tax rate, and a and b are parameters.

From equation (i)—(iii) we get

Y = a + b(Y – T) +I+ G

= a + b Y (l — t) + I + G

Or, Y a+ I+ G/1-b(1-t)

Therefore, dy/dt = -(a + I + G) b/[1-b(1-t)²] which implies (dy/dt) < 0. i.e., with the increase in tax rate national income falls. 700

1. The Income-Expenditure Approach:

Thus if we follow the income-expenditure ap­proach the equilibrium condition of national income becomes:

Y = E = C + I + G (36.1)

2. The Leakages-Injections Approach:

When we follow the leakage-injection approach we observe the following:

The identity between savings and investment that prevailed in a two sector economy (without gov­ernment) is also changed when government enters the picture. Leakages from the flow of spending still equal injections into the flow.

But two new terms now appear in our equilibrium condition, one on the left hand side and the other on the right hand side.

Now the total of savings plus tax payments must equal the total of business investment plus government pur­chases of goods and services:

S + T = I + G (36.2)

An important point may now be noted. Equation (36.2) does not mean that considered separately, savings equal investment and taxes equal government expenditure. If these equalities prevail, it will just be a coincidence. The essential identity is between leakages from and injections into the flow of spending, no matter how the two sides of the equation are constituted.

Problem 2:

In a three-sector (household, busi­ness and government) model, suppose household compensation is Rs. 760; taxes on household income is Rs. 100; government spending is Rs. 560; gross in­vestment is Rs. 110; depreciation is Rs. 40; and gov­ernment spending is Rs. 130. (a) Find GNP. NNP and household saving, (b) What leakage and spend­ing injections are there for this three-sector model? What is the relationship of these leakages and spend­ing injections?

(a) GNP Rs. 800, the sum of consumption (Rs. 560), gross investment (Rs. 110) and government spending (Rs. 130). NNP is Rs. 760 — GNP (Rs. 800) less depreciation (Rs. 40); NNP is also found by summing consumption (Rs. 560), net investment (Rs. 70) and government spending (Rs. 130). Household saving is Rs. 100, household compensation (Rs., 760) less taxes (Rs. 100) and consumption (Rs. 560).

(b) Household saving, taxes on household in­come and depreciation are leakages from the circu­lar flow, whereas gross investment and government spending are spending injections.

The Rs. 240 in leak­ages (saving of Rs. 100 plus taxes of Rs. 100 and depreciation of Rs. 40) equals the Rs. 240 sum of spending injections (gross investment of Rs. 110 and government spending of Rs. 130). Note that house­hold saving does not have to equal net investment when there is a government sector.

When we include the government sector in the theory of income determination the conditions of na­tional income equilibrium are changed. Now national income will move toward the level at which desired savings plus taxes equal desired investment plus gov­ernment expenditure.

Thus we get the following con­dition:

S^d + T = I^d + G (36.3)

The last point is very important here. It high­lights the fact that desired savings do not have to equal desired investment in order for a given level of national income to be maintained. Like the injec­tions (plans) and expectations of the private sector, government spending and taxes are very important condition of national income equilibrium:

The national income can be sustained (or main­tained) at a level at which desired savings substan­tially exceed desired investment, as long as govern­ment expenditure exceeds tax revenues by the same amount.

Problem 3:

A simple example will prove the point. Let us suppose the economy is in a situation in which desired saving equals Rs. 75 crore, while desired investment is just Rs. 60 crore. The leakages- injections approach would now tell us that aggregate demand would continue to fall until the two were brought into equality.

But the decline need not nec­essarily occur: if government expenditure is Rs. 100 crore and tax revenue only Rs. 85 crore, the gap would be covered and a sustainable level of national income achieved. Thus in terms of equation (36.3) which de­fines national income equilibrium we get:

S^d + T = I^d + G

or. 75 + 85 = 60 + 100

or. 160 = 160.

Since leakages from the flow of spending (the left hand side of the equation) are equal to injections into the flow (the right hand side of the equation), and the desires of both savers and investors are realized, a sustainable level of national income is achieved.

We also observe that this equilibrium level of national in­come is achieved with a government budget deficit of Rs. 15 crore, which is equal to the difference between desired saving and desired investment. If the imbal­ance were in the opposite direction, it would have to be corrected by a budget surplus.

Problem 4:

Find the equilibrium level of income when

S = -70+0.25Y_d.Y_d = Y-T.I = I₀ = 40.

G = Go = 30. and T = T₀ = 20.

In equilibrium, leakages from the system (S + T) are balanced by injections into the system (I + G).

S + T = I + G

-70 + 0.25Y_d + 20 = 40 + 30

But Y_d = Y – T,

-70 + 0.25(Y – 20) + 20 = 40 + 30

-70 + 0.257-5 + 20= 70

0.25Y = 125

Y = 500

The graph for this problem is found in Problem 2.14.

So the prediction is that: government fiscal policy can be used to change and sustain a level of national income consistent with high (full) employment.

Government Expenditure and Aggregate Demand:

Fiscal policy operates through a change in gov­ernment expenditure or a change in taxes or a change in both. Government expenditure is expansionary in its effect on national income and employment, while taxes are contractionary. In other words, aggregate demand is increased by government spending and reduced by taxes. But the effects are not symmetrical.

It may apparently seem that if government pur­chase of goods and services are increased by, say, Rs. 10 crore, and taxes are raised simultaneously by an equal amount, the programme will have a neutral ef­fect on the economy. In other words, there will be no net change in national income and product. But this is not true.

It is to be noted that government expenditure is likely to have a direct effect on aggregate demand.

But taxes affect consumption spending, i.e., by reduc­ing disposable income. A government purchase of medicines for distribution through hospitals, for in­stance, enables business firms to produce and employ resources in the production process.

National output and incomes are directly increased by the amount of the government purchase and that amount then has the usual multiplier effect on aggregate demand, just like an increase in private investment.

By contrast, taxes exert a direct influence on the propensity to consume rather than on aggregate de­mand as a whole. Consequently, the multiplier effect of aggregate demand is of a different magnitude. We may look at the direct effect of government ex­penditures on aggregate demand.

With government in our model of income determination, the national product or GNP has three components:

Y = C + I + G

or Y = consumption expenditure + private in­vestment + government purchase of goods and ser­vices.

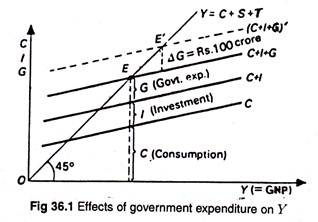
We now show how national income equilibrium is reached in our extended model. See Fig. 36.1. Here we have added to the schedule of the propensity to consume C both private investment I and govern­ment purchase of goods and services G to derive a schedule for aggregate demand. Now the level of na­tional income is determined by the intersection of that schedule with the aggregate supply schedule.

Fig. 36.1 shows that if we add government ex­penditure G to the existing C + I curve, we get a curve like C + I + G which intersects the 45° line at E. The components of total expenditure are also shown separately.

If the government spends Rs. 100 crore more, the C+I+G curve shifts to a new position (C+I+G) in our diagram. Income goes up to E’ due to a multiplier response of GNP to the new government spending.

Taxation:

Just as government expenditure is expansionary taxes are contractionary in-as-much as they reduce the disposable income of individuals and thus their capacity to spend on consumption goods.

So if private investment and government expenditure stay put at the old level, a rise in taxes will lower the C + I + G schedule and bring about a reduction in income and employment. Or, if we start with a position of infla­tionary gap, the gap will be eliminated.

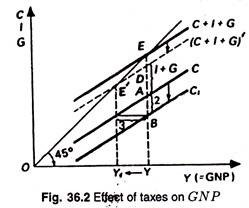
This is pic­tured in terms of Fig. 36.2. Oppositely, a cut in taxes will stimulate consumption and start off a process of recovery if we are already in deep depression. In short, a cut in taxes (if it is of a permanent nature) will act as an antidote against unemployment just as an increase in government expenditure.

A cut in taxes reduces disposable income and conversely. Here an increase in taxes lowers the G schedule. The schedule shifts to the right, i.e., it shifts downward. But the downward shift (of Rs. 2) is 66% of the rightward shift (Rs. 3) if MPC = 2/3.

Now with this downward shift of the consump­tion function, the C + I + G’ schedule is lowered to (C + I + G). And the equilibrium point shifts to the left. So a rise in taxes of Rs. 3 and the corresponding decrease in disposable income will reduce consump­tion expenditure by Rs. 2 if MPC = 2/3.

The net result is that a tax increase by reducing the value of the multiplier leads to a slowdown of the income gener­ation process. This is a leakage from the income flow. This is what is shown in the Fig. 36.2.

Some economists) however, hold the view that when increased government expenditure is added to a full-employment economy with a balanced budget; taxes will have to be increased by more than enough to balance the budget if we are to avoid an inflationary gap.

This is because the increase in government ex­penditure itself will raise income out of which an extra amount will have to be collected in taxes (in order to balance the budget).

And a cut in public spending need be supported by a sharper cut in taxes due to consequent fall in income caused by the lowering of government expenditure.