Meade’s Neoclassical Model of Economic Growth | Economics

In this article we will discuss about:- 1. Introduction to Meade’s Neoclassical Model 2. Assumptions of Meade’s Model 3. Meade’s Formal Model 4. Changes in the Rate of Economic Growth 5. State of Steady Economic Growth 6. Stability of the System 7. Graphical Representation 8. Critical Evaluation.

Introduction to Meade’s Neoclassical Model:

In his book, “A Neoclassical Theory of Economic Growth’, Prof. J.E. Meade has put forward a model intended to explain the process of equilibrium growth (i.e., the steady-state growth). In fact, the model attempts to analyze the manner in which the simplest type of classical system would behave under the conditions of equilibrium growth.

At the outset Prof. Meade states the following three principal means whereby an economy can grow:

(i) Capital accumulation resulting from the savings made out of current income. This brings about a growth in the stock of the ‘capital instruments of production’.

(ii) Growth of working population, i.e., growth of labour force.

(iii) Technical progress which permits of growth in output through time out of a given amount of resources.

He then tries to examine the manner in which a classical economic system (i.e., where perfect competition prevails) would behave if the three above explained factors were working simultaneously. To be more specific, Prof. Meade in his model analyses the manner in which a perfectly competitive economy would behave during a process of equilibrium growth when real capital is being accumulated, the labour force is growing and technical progress is occurring.

Assumptions of Meade’s Model:

1. A closed economy is assumed. That is, all types of economic and financial relationship with other economies are assumed away.

2. Complete laissez-faire is assumed to prevail in the economy and therefore there is no intervention by the government in the economy. Besides, the economy is working under the conditions of perfect competition.

3. The production in the economy is assumed to take place under the conditions of constant returns to scale. That is to say, if in a given state of technical knowledge all factors of production in an industry are increased by x per cent, then the output also increases by x per cent.

4. The economy is assumed to produce only two commodities, viz., a consumption good and a capital good. The consumption good satisfies all ultimate human needs of consumption. And the capital good is used to produce further the output of capital goods or consumption goods.

5. Machines are the only form which the capital is assumed to take. As such, the working capital in the form of goods in the process of production is assumed away.

6. Besides machines, there are two other factors of production, viz., land and labour, and they are assumed to be in a state of full employment.

7. There is assumed to be a constancy of the money price of consumption goods. That is, the cost of living index remains unchanged.

8. Like other neoclassical economists, in Meade’s model production function is assumed to be such that the substitution of one factor for another is possible. In other words, in a given state of technical knowledge, it is possible to produce the consumption good or capital good by a more labour-intensive method or a more land-intensive method or by a more capital intensive method, depending upon the relative cheapness of labour, land or capital.

9. The substitutability between machines and labour, however, is assumed to be of a special type. It is assumed that all machines are alike (being regarded simply in terms of the tonnage of steel) and the ratio of labour to machinery (i.e., of workers to tons of steel in stock) can be altered in any desired way, both in the short run and the long run. Prof. Meade calls this as the assumption of perfect malleability of machinery.

10. It is also assumed that at every moment of time, the production function for a unit of consumption good is the same as the production function for a unit of capital good. The implication of this is that notwithstanding the state of technical knowledge, the cost-price of a machine is the same as the cost-price of consumption good. Meade calls this as the assumption of perfect substitutability in production between capital goods and consumption goods.

11. Lastly, it is assumed that regardless of the length of time for which the existing machines had already been in sue, a certain percentage wears or tears out each year. For example, the existing stock of machines (measured in tons of steel) may require replacement to the extent of five per cent each year due to depreciation. Prof. Meade calls this as the assumption of depreciation by evaporation.

Meade’s Formal Model:

In the backdrop of the simplifying assumptions listed above, Prof. Meade tries to examine the system through time as the stock of machines increases, as the working population grows, and as productivity is raised by virtue of technical progress. However, the attention is concentrated only on the equilibrium growth of the system and not otherwise.

As a starting point of the model, Prof. Meade mentions the following four factors upon which the net output of the economy would depend:

1. The net amount of the stock of machines which is available to the economy at a particular time. It is ‘net’ in the sense that from the existing stock of machines, the amount of depreciation has been deducted;

2. The amount of labour available for productive employment;

3. The amount of land or natural resources available for productive use in the economy; and

4. The state of technical knowledge (which is assumed to improve through time).

Now, the relationship between the net output and its determinants can be written in the form of a simple production function as–

Y=F (K, L, N, t)

where Y stands for the net output (or national income), K is the existing stock of machines, L is the amount of available labour force, N is the amount of land and t is the time which signifies technical progress as it (i.e., technical progress) is supposed to occur merely with the passage of time and permits the increase in net output without any increase in K, L, or N.

As is clear from the production function, net output can increase in any one year due to the growth of K, L, N or t. But if it is assumed that the amount of land or natural resources available to the community remains unchanged (so that there is no change in land (to affect the level of net output Y), then the growth of net output will be entirely due to the growth of K, L, or t. We may, therefore, express the total change in net output as equal to the sum of the changes in output arising from these three influences taken separately. That is–

∆Y=V ∆K + W ∆L + ∆Y’

What this equation really means is that the annual increase in the net output (∆Y) is equal to the increase in the stock of machinery (∆K) multiplied by its marginal product (V) plus the increase in the amount of labour (∆L) multiplied by its marginal product (W) plus the increase in the rate of annual output due simply to technical progress (∆Y’).

Now, the annual proportionate rate of growth of output can be determined by dividing both sides of the above equation by Y and making some meaningful adjustments.

Thus, we have–

 

Where,

∆Y/Y= annual proportionate rate of growth of output,

∆K/K= annual proportionate rate of growth of the stock of machinery,

∆L/L= annual proportionate rate of growth in the working population, and

∆Y’/Y = annual proportionate rate of growth of output due simply to technical progress.

Let us denote the above four proportionate rates of growth by the symbols y, k, I and r respectively. Further, let us call VK/Y, which is the proportionate share of capital in output as U and WL/Y, which is the proportionate share of labour in output as Q. Using these notations, we can rewrite the basic relationship in the following way-

y = Uk+ Ql + r

This shows that the growth rate of output (y) is the weighted sum of the three other rates of growth. More specifically, the growth rate of output is the sum of the growth rate in the stock of machines (k) weighted by the marginal importance of machinery in the productive process (U) plus the growth rate of labour force (l) weighted by the marginal importance of labour in the productive process (Q) plus the growth rate of technical progress (r).

Now, to be able to gauge the real growth of the economy, we must express our basic relationship, viz, y= Uk+ Ql + r in such a way as to allow for the growth of population. Only then we can have a true index of the growth of real income per head. In other words, when we subtract the population growth from the income growth then we can get the growth in real income per head from our basic relationship. For instance, if the income (y) increases by 10 per cent per annum and at the same time population (I) grows by 2 per cent per annum, then the real income per head will rise by (y – I), i.e., 10-2 = 8 per cent per annum. Thus, subtracting the population growth (I) from the income growth (y) to get the real income per head, we can write the basic growth relationship in the following form–

y-l = Uk – (1 – Q)l + r

This equation tells us that the growth in real income per head (y – I) is the outcome of three factors – two of which tend to raise it, while the third works to decrease it. The factors which tend to raise the real income per head are– first, the growth in real capital (k) weighted by its proportional marginal product (U), and second, the rate of technical progress (r).

On the other hand, the force which tends to depress the per capita real income is the growth rate of population (I) weighted by one minus the proportional marginal product of labour, i.e., (1 – Q). This depressant factor, viz, (1 – Q) I is simply expressive of the familiar tendency for the diminishing returns to set in when increasing amounts of labour are applied on a given amount of land and capital equipment.

It can also be possible to incorporate the variable of savings in our basic growth relationship. We know that and U = VK/Y and k = ∆K/K .Now, if S is the proportion of the net national income which is saved, then the total savings out of national income would be SY and this must be equal to ∆K, the addition to the stock of capital made thereof. Hence, we can write, k = SY/K, where SY represents the amount of net real income which is added to the stock of machines through savings over the course of a year so that Uk = (VK/Y). (SY/K) =VS. We may, therefore, rewrite our basic growth equation in the following alternative way–

y – l = SV – (1 – Q)l + r

Changes in the Rate of Economic Growth:

Having examined the main determinants of the rates of growth of real income per head, Prof. Meade proceeds to study the conditions under which the growth rates would tend, by itself, to rise or fall over time. More exactly, Prof. Meade, now, tries to answer the question– “Is growth likely to feed on itself and to become more and more rapid or is it likely to become less and less rapid and peter out as the economy develops?”

To be able to pick out the factors crucial to the changes in the rate of economic growth, Prof. Meade concentrates on a limited number of relationships. And for that purpose, he assumed that the growth rates of population and technical knowledge (i.e., I and r) in our basic growth relationship are given and constant—having been assumed to be determined by exogenous non-economic forces.

Once we grant that I and r are given and constant, it is evident from our basic growth equation, viz., y – l = SV – (1 – Q)l + r, that whether with passage of time (y -I) will rise or fall would depend on the behaviour over time of V, S and Q. Now there are four major considerations which would govern the behaviour over time of V, S and Q. They are as follows–

First, if there is no technical progress and population growth, a rise in the rate of savings would cause the capital per head to increase with the resultant effect of lowering down the marginal product of capital (since there would be diminishing returns to a single factor of production). That is, V would fall. However, this decline in V would be lesser if the elasticity of substitution between machinery and other factors (labour and land) is greater.

Second, technical progress would cause V to rise over time. New technical knowledge and inventions would bring forth more profitable channels for new capital investment. So that, a given proportion of income saved would give rise to an increasing rate of growth in real income per head. As such, the rate of technical progress would tend to offset the depressing effect upon the level of V, caused by the diminishing returns to capital accumulation.

Third, the nature and extent of technical progress exerts a very important influence on the growth rate of real income per head over time. Whether or not the technical progress raises the marginal product of all factors simultaneously would depend on its nature. A rapid rate of neutral technical progress could indeed do so. However, as it is, the technical progress may be biased in favour or against a particular factor. And it may, therefore, make that factor more or less important at the margin over time.

Now, suppose that in an economy capital is being accumulated more rapidly than the growth of population. And if at the same time technical progress is biased in favour of capital relatively to labour then this will further go to raise the rate of growth of output per head with the passage of time. It is because the nature of technical progress is such as to raise progressively the productivity of capital which by assumption is being accumulated rapidly. And the fact that technical progress is such as to diminish the relative importance of labour at the margin would be of no great consequences as by assumption the growth rate of population in the economy is quite low. Under these conditions, V would tend to rise and income per head over time would rise. And this, in turn, would raise S.

Fourth, a change in the distribution of income may cause the proportion of national income saved to rise or fall.

Assume that:

(i) Savings out of profits are larger than out of wages,

(ii) Capital is being accumulated at a rate higher than that of population;

(iii) There is a high elasticity of substitution between machinery and labour; and

(iv) The technical progress is biased in favour of capital.

Under these conditions, the income distribution would change towards larger profits so that there is a tendency for S to rise still further.

There are two valid reasons for one to expect a large proportion of national income going to profits than to wages under these circumstances.

First, since the per head availability of machinery increases and because of the high elasticity of substitution between the two factors, neither the profit per machine would fall rapidly nor the real wage of workers rise rapidly.

Second, the nature of technical progress being such as to raise the productivity of capital, the rate of profit would tend to rise relatively to the real wage rate.

With these, therefore, following the change in income distribution towards larger profits, there will be a tendency for S to rise. As such, the element VS, in the determination of the rate of growth of the economy, will tend to rise with the passage of time.

In order to be able to appreciate the above explained set of four considerations, in so far as they influence the changes in the rate of growth over time. Prof. Meade considers the special case where population is constant (i.e., l = 0). In this view, our basic growth relationship becomes–

y = VS + r

Evidently, in this situation, the rate of growth of real income depends upon capital accumulation (VS) and technical progress (r). Further, if the rate of technical progress (r) were constant, the growth rate of real income per head will depend simply upon whether VS will be rising or falling with the passing of time.

Now what are the factors which determine whether VS will be rising or falling through time? Prof. Meade, in fact, enumerates on the basis of an exercise, the factors which, with a constant population, might cause VS to rise over time so that economic growth becomes self-sustaining and continually accelerating.

They are:

(i) The prevalence of a high rate of technical progress,

(ii) The machine-using nature of technical progress,

(iii) Initially a low proportion of savings out of income,

(iv) A high elasticity of substitution between machinery on the one hand, and labour and land on the other,

(v) An increasing proportion of income saved as the real income rises, and

(vi) Along with the change in income distribution in favour of profits brought about by (ii) and (iv) above-an especially large proportion of profits channelled to savings.

The State of Steady Economic Growth:

Having examined the factors which, with a constant population, may condition economic growth in such a way that it feeds upon itself and continues to accelerate in speed, Prof. Meade proceeds to analyze the circumstances which would establish a path of steady-state economic growth. To do so, the assumption of constant population is given up. Rather we return to our original assumption that it is growing at a constant proportionate rate I. However, we continue to assume that the rate of technical progress is constant.

Now, the steady state of economic growth is that state wherein the growth rate in total output (y), as also the growth rate in income per head (y-l) is constant. In fact, with our assumption of a constant growth rate of population (I), the growth rate in income per head (y-l) will be constant only when the growth rate of total output (y) is constant.

Prof. Meade, then, shows that given the constant proportionate growth rate of population (I), and a constant rate of technical progress, the following conditions have to be met if a constant growth rate of total output, i.e., a steady state of economic growth is to be achieved.

These conditions are as follows:

(i) All elasticities of substitution between the various factors must be equal to unity,

(ii) The technical progress must be neutral towards all factors, and

(iii) The proportions of savings out of profits, wages and rents are all constant.

The implication of the condition (i) is that if all the elasticities of substitution between our three factors—land, labour and machinery—are equal to one and if there are constant returns to scale, then no change whatsoever in the factor supplies would cause any change in the distribution of national income as between the three factors of production. Actually, any possible change in the relative amount of the factors of production would get compensated by the opposite changes in their relative rates of remuneration.

Condition (ii) simply states the definition of that type of technical progress which has no effect whatsoever upon the proportions of national income going to profits and wages.

The conditions (i) and (ii) taken together ensure that the proportions of national income going to profits (U), wages (Q), and rents (Z), would remain constant during the process of economic growth.

Now, since U is the proportion of profits out of the total national income Y, therefore, the total profits will be UY. And since S_ν is the proportion of profits to national income saved, therefore, S_νUY represents the total savings out of profits. In the same way, S_wQY and S_gZY represent respectively the total savings out of wages and rents. But the aggregate savings in the economy are given by SY, where S represents the proportion of the total national income saved. As the aggregate savings of the economy must be equal to the sum of the savings out of profits, wages and rents, we, therefore, have-

S=S_νV + S_wQ+ S_gZ

With U, Q, Z, S_ν, S_w, and S_g being all constants vide conditions (i), (ii) and (iii); it follows that S, the ratio of total savings to total national income, will also be constant. Actually, the above equation tells us that the ratio of total savings to total national income (S), is the sum of the constant proportions of savings out of profits, wages and rents (S_ν, S_w and S_g), each respectively weighted by the constant proportions of the national income going to profits, wages and rents (U, Q and Z).

Let us now consider our basic growth relationship represented by the equation-

y=Uk +Ql+ r

In this equation, we know I and r are constant by assumption. And also U and Q are constant vide conditions (i) and (ii). As such y will be constant only if k is constant.

Now, we know k, the growth rate of the capital stock, equals SY/K. But S is a constant. Hence, k will be constant only if Y/K, i.e, the ratio of annual national income to the value of the stock of capital, is constant. Again, Y/K will be constant only if the rates of growth of Y and K are the same. That is to say, Y/K will be constant only if y = k.

(Note that y and k represent rate of national income or output and capital respectively)

Thus, we find that the growth rate of income will be constant only when the growth rate of capital stock is equal to the growth rate of the national income.

In this view, therefore, the conditions under which the growth rate of income will be constant are simply given by the conditions under which the growth rate of capital stock equals the growth rate of the national income. There would be some level of the growth rate of the capital stock which equalizes the growth rate of national income with that of the capital stock.

Prof. Meade calls this as the critical growth rate of the capital stock. The equality between y and k would fail to be achieved if the growth rate of capital stock were more or less than this ‘critical growth rate’. Now, if we use ‘a’ to designate the ‘critical growth rate’, then we can write our basic relationship in the following way-

a = Uq + Ql + r

or a = (Ql + r) / 1 – U

That is, if the growth rate of capital stock is (Ql + r) / (1 – U), the then growth rate of national income would also be (Ql + r) / (1 – U) and it would remain constant at this level.

Stability of the System:

We have seen that the economy is in its state of steady growth so long as the rate of growth stock of capital stock k or (SY)/K is at its critical or equilibrium level of (Ql +r) /(1 – U). But the growth rate of the capital stock will attain its critical level of if (Ql +r) / (1 – U) and only if the savings of the various recipients happen to be just and only just enough to make the existing stock of capital grow at the rate (Ql +r) / (1 – U).

Now it remains to be seen whether the system can be stable in this state of steady growth level? That is, if the growth rate of capital stock (SY)/K were greater or lesser than the critical level, will certain forces set in, to bring back (SY)/K to the equilibrium level given by (Ql +r) /(1 – U) ? It can be shown that the system would, indeed, be stable.

Suppose first that, (SY/K) > (Ql+ r)/(1 – U). In this case, it can be seen from our basic relationship y = uk + Ql + r, that if k or SY/K is above the critical level ‘a’ by say an amount x, then the value of y will be raised above the critical level ‘a’ by only a fraction U of x. Therefore, in the case when the growth rate of capital stock exceeds the critical value, income will grow at a rate lesser than the growth rate of capital stock. In consequence thereof the savings will fall. This, in turn, would bring down the growth rate of capital. As such SY/K would continue to decline till it reaches the critical level.

Similarly, if (SY/K) > (Ql+ r)/(1 – U); the system would regain its equilibrium level. It is because, in this case, income would grow more rapidly than the capital stock with the result that savings would grow more rapidly than the capital stock. In consequences thereof, the rate of growth of the capital stock would rise till it reaches the critical level.

To sum up, given that I and r are constant, all the elasticities of substitution between various factors are equal to unity, technical progress is neutral towards all factors and the proportion of savings out of profits, wages and rents are all constant, then the growth rates of national income and of the capital stock would both converge towards the constant level of (Ql+ r)/(1-U).

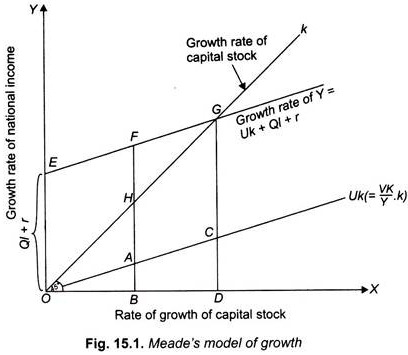
Graphical Representation of the Meade’s Model:

The basic argument of Prof. Meade’s model can be explained with the help of the geometrical construction shown in Fig. 15.1. In this diagram we measure the growth rate of the capital stock along the horizontal axis. And the growth rate of national income is measured along the vertical axis. The line OAC drawn through the origin with a slope U, represents the proportional share of capital in national income. The line EFG, drawn at a distance Ql + r from the origin and parallel to the line OAC, represents the total growth rate of the national income. The 45° line Ok gives the growth rate of the capital stock.

If, to start with, the actual growth rate of the capital stock were OB, then the corresponding growth rate of national income would be BF (or BA + FA). In this, BA represents that part of the growth rate of national income which is attributable to the accumulation of capital stock.

And FA (= OE = Ql + r) would represent that part of the growth rate of national income which is on account of labour growth and technical progress. But at the point F, FB > FA, i.e, the growth rate of national income is greater than the growth rate of the stock of capital or y > k. As such, k will start rising till finally the point D on the horizontal axis is reached. It is only then that the equality between y and k would be reached at the point G on the 45° line. That would represent the steady state of economic growth.

We can also derive the value y and k for ‘steady growth rate’ from this diagram. Since CD = Uk and GD = k, therefore, GC must be equal to GD – CD or k- Uk= (1 – U) k.

i.e., GC= (1 – U) k

But GC = OE = Ql + r

.^.. for equilibrium growth rate (1 -U) k = Ql + r

or k = (Ql+r)/(1 – U), which is the value that y and k must have in the state of steady economic growth.

Critical Evaluation of Meade’s Model:

Prof. Meade’s model illustrates the manner in which the simplest form of neoclassical system with perfect competition and constant returns to scale would behave during the process of equilibrium growth. This in itself represents a major achievement as it enables the examination of the process of change in the variables of a simple neoclassical system over time. All the previous works had only attempted to compare two static positions of the neoclassical system. Having introduced the dynamic dimensions in the neoclassical system, Prof. Meade succeeds in bringing out the implications of the neoclassical analysis for economic growth in general and for steady state in particular.

By explaining a neoclassical system with perfect atomistic competition where capital is being simultaneously accumulated, working force is growing and technical progress is taking place, Prof. Meade provides a deep insight into the mechanism underlying the process of economic growth. The results so obtained in this model could well be modified by allowing for the effects of certain types of imperfect competition so as to bring them nearer to reality. Indeed, the main merit of Prof. Meade’s model lies in the lucid manner in which his model demonstrates the simultaneous influence of capital accumulation, population growth and technical progress on the growth rate of national income and the standard of living over time.

Prof. Meade’s exposition of steady state of economic growth is, in fact, a replica of Mrs. Joan Robinson’s ‘Golden Age’. But the merit of the former over the latter lies in the fact that it explains the same thing without having to make the unrealistic assumption of full employment of capital and labour. Mrs. Robinson’s treatment of ‘Golden Age’ is tenable only under this assumption.

However, Prof. Meade’s model captures but only a patch of reality and that too under rather limiting conditions. It completely neglects the influence of social, political and international factors in economic growth. A crucial weakness of Prof Meade’s model stems from his assumption of the constant money prices of consumption goods as being ensured just through the operations of monetary policy.

And that the adjustments in money wage rates ensure full employment. But it is quite unrealistic to assume that the easing or tightening of monetary conditions could, in fact, be carried out with all that foresight and precision as is called for by Prof. Meade’s model. Mrs. Robinson, in fact, dubbed Meade’s model as simply ‘pseudo-casual’.

Again, Prof. Meade’s contention, namely, ‘the cost-price of a capital good remaining the same as the cost price of a consumption good being based on the assumption of ‘perfect’ substitutability in production between capital goods and consumption goods’ and the ‘perfect malleability of machinery’, is not only unrealistic but also self-contradictory. Even under these extremely hypothetical assumptions, it is possible that the price of capital goods may vary relatively to the price of consumption goods. For instance, if the nature of technical progress were such that it tended to reduce the real cost of consumption goods more quickly than that of capital goods, the price of the capital goods may rise.

Also, a relative shift of demand away from the consumption goods onto capital goods; would result in a shift of the factors of production away from the production of consumption goods onto the production of capital goods. In consequence, the factor intensities of the two industries producing capital goods and consumption goods would come to differ. This may cause the cost price of capital goods to change relatively to that of consumption goods.

However, despite the above limitations Meade has carried further neoclassical approach and made it quite generalised.