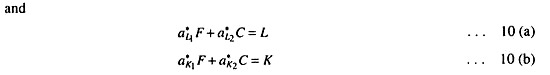Stolper-Samuelson Theorem (SST) | Theorems | Economics

The Stolper-Samuelson theorem (SST) simply suggests that, in any particular country, a rise in the relative (producer) prices of the labour intensive good will make labour better off and capital worse-off, and vice-versa, provided that some amount of each good is being produced.

The SST of a Linear Model:

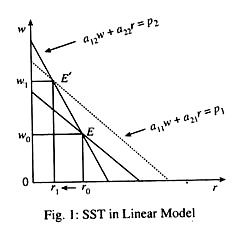
Here we assume the economy produces two goods, labour and capital. The food industry in labour-in­tensive and, the cloth industry is capital-intensive. In Fig. 1 we show the SST in linear model. Here we have linear constraints

a ₁₁ w + a₂₁r = p₁ … (1)

a₁₂w + a₂₂r = P₂ … (2)

These are zero-profit conditions. Here a₁₁ is the amount of labour required to produce 1 unit of cloth, a₂₁ is the amount of capital required to produce 1 unit of cloth, w and r are the prices of two factors (labour and capital) and p₁ is the price of cloth. The same is the case with food. Eqn. s (1) and (2) are the zero-profit conditions.

The slopes of the lines shown in Fig. 1 depend on factor intensities expressed by input- coefficients (a₁₁, a₂₁….etc.). For cloth the slope of the zero profit equation is-a₁₁/a₂₁. For food the slope is – a₁₁ a₂₂. Here we have assumed that cloth (C) is capital-intensive and food (F) is labour-intensive.

Under these conditions an increase in p₂ (the price of cloth) which causes a parallel shift of unit (2) produces a new solution at E’. This lowers r and raises w. Thus if the price of, say, the labour intensive good (food) rises, the price of labour (the wage rate) will rise, while price of the other factor, (capital) will fall.

In short, if the price of capital intensive cloth (p₂) rises then the price of capital (r) increases while the price of labour (w) falls. Likewise, if the price of labour-intensive good food (p₁) rises the price of capital face while the price of labour increases.

The SST states that if, say, the price of capital-intensive good rises r will not only rise but will rise in greater proportion to the output price increase. The price of the other factor falls but not necessarily in greater proportion to the rise in output price.

Here we use the indirect national income functions which shows the maximum value of NNP for given output prices and factor endowments.

We assume that NNP (say, Y) is a linear for of output levels:

Y = p₁ F + p₂ C … (1)

where F and C are foods and cloth; respectively and p₁ and p₂ are their prices.

We may now maximise M by first maximising the two square-bracketed terms (which enter negatively) w.r.t 5 the a_iJ’s, treating the o/t levels of F and C as constants.

This is equivalent to two separate minimisations:

Here (a_L1 , a*_K1) &(a*_L2, a*_K2) are cost-minimising input combinations. Equations 9 (a) and 9 (b) are zero-profit conditions, i.e., price of each commodity is equal to its cost of production (which is the sum of labour-cost and capital cost).

Equations 10 (a) and 10 (b) are the endowments of the two factors (capital and labour).

We may now examine the effects of changes in output prices on factor prices.

Equations 9 (a) and 9 (b) are the sole determinants of factor prices.

Since, a _ji s are functions of w/r alone, the solution values of these two equations are:

w=w*(p₁, p₂) … 11(a)

r = r*(p₁, p₂) … 11(b)

We may now differentiate 9 (a) and 9 (b) w.r.t p₁ after substituting equans 11 (a) and 11 (b) into 9 (a) and 9 (b) for w and r, respectively, factor prices are also functions of factor prices.

So, upon differentiating 9 (a), we get

This means that if one country is more labour intensive than the other, i.e., its K/L ratio is lower than the ratio in the other country, then the equations defining factor prices as function of old price will be well-defined. Moreover, the comparative static results (1 b), indicating the response of factor prices to changes in output prices, will be well-defined.

Suppose now that industry 1 is more labour-intensive- i.e.,

Then A > 0 and from 16 (a) and 16 (b) we get

∂w/dp₁ > 0 … I9 (a)

and ∂r/∂p₁< 0 … 19(b)

These results are the general SST. They suggest that if the price of food increases, the wage rate will rise, whereas the price of capital r will fall. If _P1 rises, F increases and C falls, i e ∂F/∂p₁ > 0 and ∂C/d_P1< 0. As food industry expands and cloth-industry contracts, there is a net increase in the demand for labour and a fall in demand for capital.

However, the price of labour (w) rises while the price of capital r falls. As a general rule, the price of a factor of production will rise if the price of the industry in which that factor is most intensively used rises and it will fall if the price of the product of industry which is less intensive in that factor rises.