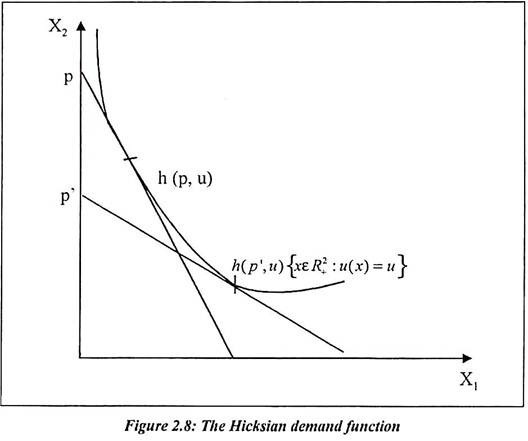
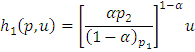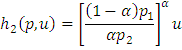The Hicksian Demand Function: With Diagram | Utility | Microeconomics

The Hicksian welfare measures can be used for the evaluation of any change of state as long as the agent’s indirect utility for income is well defined before and after the change. The set of optimal commodity vectors in the EMP is denoted as h(p,u) ⊂ R^L₊. It is known as the Hicksian or compensated demand corresponding or function if single valued. The figure shows the solution set h (p, u) for two different price vectors p and p’.

The basic properties of the Hicksian demand function is explained as follows:

Suppose u (.) is a continuous utility function representing a locally non satiated preference relation ≥ defined on the consumption set X = R^L₊. Then for any p » 0, the Hicksian demand correspondence h (p, u) possesses the following two properties. Homogeneity of degree zero in P follow because the optimal vector. The minimizing p.x is subject to u(x) ≥ u. It is same as that for minimizing ∝p.x. It is subject to this constraint for any scalar ∝ > 0.

We will explain properties and proof in the following paragraph:

Property 1:

No excess utility for any xϵh (p, u), u(x) = u

Proof:

This property follows from continuity of u (.). Suppose there exists an xϵh (p, u), such that u(x) > u.

If we consider a bundle x’= ϵ x, where ∝ϵ (0, 1). By continuity for ∝ close enough to 1.u (x’) ≥ u and p.x’ < p.x1 contradicting x being optimal in the EMP with required utility level u.

Property 2:

Convexity/Uniqueness:

If ≥ is strictly convex, then u (.) is strictly quasi-concave. Then there is a unique element in h (P, u).

If there is utility function u(x₁, x₂) = ∝ In x₁+ (1-∝) lnx₂. Then substituting x₁ (p, w) and x₂ (p, w) into u(x) we have,

As the UMP, when u (.) is differentiate, the optimal consumption bundle in the EMP can be characterizing using first order condition. The first order condition bears a close similarity to those of the UMP.

Proposition 1:

If we assume that u (.) is differentiable and it shows that the first order condition for the EMP as follows:

And

For some λ ≥ 0, compare this with the first order conditions for the UMP.

Using above proposition, we can relate the Hicksian and Walrasian demand correspondence as follows:

The first of these relations explains the use of the term compensated demand correspondence to describe h (p, u). Suppose if the price change, h (p, u) gives the level of demand that would arise if the consumers wealth were simultaneously adjusted to keep his/her utility level at u. Government helps consumer through subsidized goods. In India, it is done through public distribution system. This type of wealth compensation to consumer is depicted in above diagram. It is known as Hicksian wealth compensation.

Above diagram shows that consumers initial situation is the price wealth pair (p, w); prices then change to p’, where p^’₁ = p₁ and p^’₂ > p₂.

The Hicksian wealth compensation is defined follows:

Therefore the demand function h (p, u) keeps the consumer’s utility level fixed as prices change. In contract with the Walrasian demand function it keeps money wealth fixed but allows utility to vary.

As with the value functions the EMP and UMP, the relations allow us to develop a tight linkage between the properties of the Hicksian demand correspondence h (p, u) and the Walrasian demand correspondence x (p, w).

Hicksian Demand and the Compensated Law of Demand:

The property of Hicksian demand is that it satisfies the compensated law of demand. The price and demand of commodities move in opposite directions. The price change is accompanied by Hicksian wealth compensation.

Proposition1:

If u (.) is a continuous utility function representing a locally no satiated preference relation ≥ and that h (p, u) consists of a single element for all p » 0.

Then the Hicksian demand function h (p, u) satisfies the compensated law of demand:

For all p’ and p”,

Proof:

For any pk”o, consumption bundle h (p, u) is optimal in the EMP and so it achieves a lower expenditure at prices p than any other bundle that offers a utility level of at least u.

Therefore:

and

Subtracting these two inequalities yields the results.

Hicksian Demand and Expenditure Functions for the Cobb-Douglas Utility Function:

If we assume that the consumer has Cobb-Douglas utility function over the two goods. That is u(x₁,x₂) = x₁^a x₁^1-a. By deriving the first order conditions for the EMP and substituting from the constraints u (h₁ (p, u), h₂ (p, u) = u, we obtain the Hicksian demand functions.

&

If we calculate it as follows:

E (p, u) = p.h (p, u) yields the following equation

Above function is Hicksian demand and expenditure functions for the Cobb-Douglas utility function.