Optimisation techniques are an important set of tools required for efficiently managing firm’s resources.
In what follows we will focus on the use of differential calculus to solve certain types of optimisation problems.
Differential Calculus: The Concept of a Derivative:
When a change in the independent variable, that is, ∆X gets smaller and approaches ∆Y zero, ∆Y/ ∆X becomes better approximation of the slope the function, Y = ƒ (X), at a particular point.
Thus, if ∆X is infinitesimally small, ∆ Y/ ∆X measures the slope of the function at a particular point and is called the derivative dY/dX of the function with respect to X. The derivative or dY/dX or more precisely the first derivative of a function is defined as limit of the ratio ∆Y/∆X as ∆X approaches zero. Thus
It is thus evident that derivative of a function shows the change in value of the dependent variable when change in the independent variable (∆X) becomes infinitesimally small. Note that derivative of a function [Y = ƒ(X)] is also written as d (ƒX)/dX or ƒ(X).
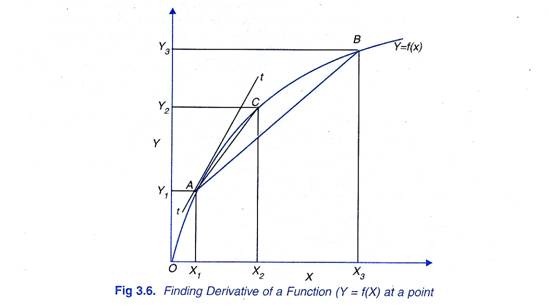
The derivative of a function at a point measures the slope of the tangent at that point. Consider Figure 3.6 when ∆X = X3 – X1, the slope of the corresponding straight line AB is equal to Y3-Y1 /X3– X1 .When ∆ X becomes smaller and is equal to X2 – X1 slope of the corresponding line AC is equal Y2-Y1/ X2 –X1. It will be seen from Figure 3.6 that slope of line AC is more near to the slope of the tangent tt drawn at point A to the function curve.
Similarly, if AX is reduced further, slope of the straight line between the two corresponding points will go on becoming closer and closer to the slope of the tangent tt drawn at point A to the curve. At the limit of ∆Y/∆X when ∆X approaches zero, slope of the tangent such as tt at a point on a function becomes the derivative of the function with respect to X.
ADVERTISEMENTS:
Thus, derivative dY /dX is slope of a function whether it is linear or non-linear and represents a change in the dependent variable due to a small change in the independent variable. The concept of a derivative is extensively used in economics and managerial decision making, especially in solving the problems of optimisation such as those of profit maximisation, cost minimisation, output and revenue maximisation.