Creation of Money by Commercial Bank

The Creation of Money by the Banking System:

We want to show how the commercial banks are able to create money or credit against deposits through the bank multiplier. By credit, we mean granting loans and advances made by banks to the public. And, creation of money or credit refers to the multiplication of loans and advances.

As ‘every loan creates a deposit’, credit creation by commercial banks refers to the multiplication of original bank deposits. Thus, “Banks are not merely purveyors of money, but also, in an important sense, manufacturers of money.”

Banks create deposits via lending. Instead of giving loans in cash, banks issue cheque against the name of the borrowers. Now the borrower is free to draw upon his money by drawing cheques upon the banks. The people who receive the cheque deposit them in another bank. However, the bankers know that the amount of money that the depositors withdraw soon returns to the bank.

Banks also know that all the depositors will not withdraw their entire deposits at a particular time. To meet this debt obligation (in order to achieve liquidity), bankers keep certain cash balances with the central bank. This is called the legal minimum cash reserve. Let us assume that bankers maintain a 10 p.c. cash reserve with the central bank. Banks can now lend up to 90 p.c. to the public.

(a) The Money Multiplier:

No commercial banks can create money since bankers lend money that they receive from other individuals. However, even though each bank lends money to someone else what it receives, the banking system as a whole creates money.

To explain the process of credit creation, let us consider the following example:

We assume first that banks have two types of assets—legal minimum cash reserve ratio, and loans and advances to the public (to earn profit). We assume that there is no leakage of cash (i.e., no drainage of cash outside the banking system). Further, we assume that cheque transaction takes place.

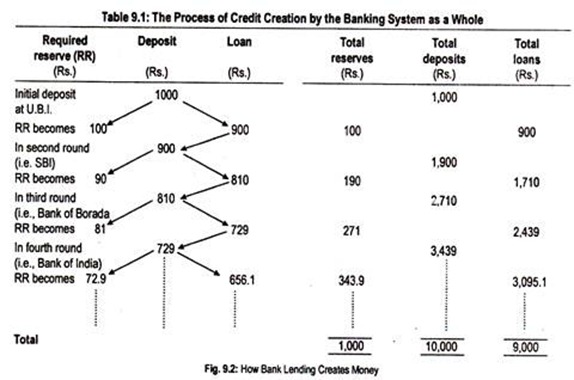
Suppose that Mr. ‘A’ deposits Rs. 1,000 in the United Bank of India. With a required reserve ratio of 10 p.c., the UBI keeps Rs. 100 as cash reserve and can lend Rs. 900 to Mr. B. Mr. B uses this money to buy goods valued at Rs. 900 from Mr. C who deposits the same in the State Bank of India.

The SBI has now a deposit of Rs. 900, new legal cash reserve of Rs. 90 and new loans of Rs. 810. The SBI now gives loans to customer Mr. D who uses it to buy goods from seller Mr. E who deposits his cheque of Rs. 810 in the Bank of Baroda, and so on.

This bank puts 10 p.c., i.e., Rs, 81 of its increase in deposits as legal minimum cash reserve and lends Rs. 729 to individual G, and so on. The process of lending of 90 p.c. of new deposits is repeated till the final deposit becomes too small to create any fresh loans.

The entire operation can be summed up in terms of Table 9.1.

The total increase in money supply (∆M) due to a deposit of Rs. 1,000 is given by the following equation:

∆ M = Rs. 1,000 + 900 + 810 + 729 … + ∆ M = Rs. 1,000 [1 + 0.9 + (0.9)² + (0.9)³ + …. + (0.9)ⁿ]

The geometric series in the brackets can be summed up to give:

∆M = Rs. 1,000 (1/1 – 0.9)

∆M = Rs. 10,000

Thus, with a cash reserve of 10 p.c., a deposit of Rs. 1,000 results in a Rs. 10,000 increase in money supply. So the credit multiplier is 10. This is the mechanism of deposit multiplication through the process of credit creation.

The formula for the credit multiplier is:

∆ M = ∆ D. 1/r

Or, ∆M/∆D = 1/r

where ∆ D stands for original deposit and r stands for legal minimum cash reserve ratio. The smaller the ‘r’, the higher is the value of credit multiplier. If ‘r’ is raised, the credit or deposit multiplier will be weaker. In short, banks can create deposits through lending much more than their original amount of deposits.

(b) Algebraic Treatment:

The above result can be demonstrated algebraically. Excess reserves—the difference between actual reserve and required reserve—form the basis of monetary expansion through bank lending. Banks have to maintain legal reserve requirements stipulated by the central bank.

Any bank that holds money more than legal reserve ratio can make loans. This amount may be called excess reserves.

If Re. 1 is deposited in a bank, the value of the second deposit, symbolized by ‘d’, will be equal to the excess reserves created by first deposit:

D = 1-r

where r is the minimum cash reserve. The value of the third deposit will be the value of the second deposit, d, minus the legal cash reserve on the second deposit, i.e.,

d (1 -r) = d²

The value of the fourth deposit will be equivalent to the value of the third deposit, d², minus the required reserve on the third deposit, i.e.,

d² (1 – r) = d³

and that of the fifth deposit

d³ (1 – r) = d⁴

The sequence of this infinite but diminishing chain of deposit creation and, hence, change in total money supply, ∆M, after n deposits resulting from a deposit of Re. 1, is:

∆ M = 1 + d + d² + d³ + d⁴ + … + d^{n -1}

Since r < 1, the sum of this geometric progression taken to an infinite number of periods may be found by the formula

∆M = 1/1 – d

We know that d = 1 – r. The above equation then reduces to

∆M = 1/1 – 1 + r = 1/r

Let the primary deposit be ∆ D.

Therefore,

∆M = ∆D. 1/r

This effect is known as bank multiplier or deposit multiplier or money multiplier.

Assuming r = 1/10 (i.e., 10 p.c.), the value of bank multiplier becomes 10. This means that an increase in initial deposit of Rs. 1,000 causes total deposits or money supply to rise by Rs. 10,000. The initial deposit thus has “multiplier” effect on money supply. The credit multiplier is then defined as the total increase in money supply divided by the increase in deposit, i.e.,

∆M /∆D = 1/r

The deposit multiplier (or money multiplier) is equal to the reciprocal of minimum cash reserve ratio. If r = 0.2, the credit multiplier would be 5. This means money supply increases by Rs. 5 for each one rupee increase in deposit.

Limitations:

However, commercial banks can never create credit to such an extent as described above.

In reality, the power of commercial banks to create credit is subject to the following limitations:

(a) Leakage of Cash:

In the process of credit expansion outlined above, we assumed that there is no leakage of cash, i.e., the amount lent by one bank is immediately deposited in another bank.

Let us now assume that cash leaks out of the banking system. This means that the borrowers do not deposit the entire amount of sanctioned loans. A part of the loaned amount is deposited. This will cause multiplier effect to become weaker than the full money multiplier described above.

(b) Preference for Liquid Cash:

The credit creating capacity of banks greatly depends on the desire of the public to hold cash. If people use more cash rather than cheque, the banks will be left with a smaller amount of credit deposit and, consequently, the process of credit creation will slow down.

(c) Central Bank’s Influence:

We know .from the credit creation formula that the value of the deposit multiplier depends on the value of V. This V or the required cash reserve ratio is determined by the central bank of a country. If it is raised by the central bank, credit creating power of the commercial banks will be smaller and, hence, the multiplier will be weaker.

Furthermore, the credit-creating potential of banks is restricted by the central bank’s credit control policy. The central bank—by increasing bank rate or conducting open market sales of securities—may curb the lending capacity of commercial banks. Consequently, total credit expansion will be much less than before.

(d) Business Conditions:

Again, credit creation depends upon the business conditions prevailing in an economy. If business conditions look unfavourable, people will take fewer loans and advances from the commercial banks. Thus the total volume of money supply will be smaller. Larger credit expansion is possible only in periods of prosperity.

Despite these limitations, there is no doubt that commercial banks can and do create credit and thus increase the supply of money in an economy.