Notes on Adverse Selection | Microeconomics

Let us suppose that each consumer wants to buy an umbrella and that there are two different qualities available.

Consumers are willing to pay Rs 75 for each high-quality umbrella and Rs 45 for each low-quality umbrella. It is impossible to tell the quality of umbrellas in store. This can only be determined after they are used. Let us suppose further that both high and low-quality umbrellas cost Rs 65 to manufacture and that the industry is perfectly competitive.

We have to determine the expected quality of umbrellas produced. We shall suppose that consumers judge the quality of the umbrellas available in the market by the average quality sold, just as in the case of the lemons market.

If the fraction of high- quality umbrellas is q, then the consumer would be willing to pay for an umbrella the price:

p = 75 q + 45 (1 – q), which is the weighted average of the prices offered for high-quality and low-quality umbrellas.

We have to consider here the following three cases:

(i) Only low-quality manufacturers produce. In this case, the consumers would be willing to pay only Rs 45 for an average umbrella. But it costs Rs 65 to produce an umbrella. So none would be sold.

(ii) Only high-quality manufacturers produce. In this case, the price of an umbrella would come down to the level of marginal cost, i.e., Rs 65, because of competition among the producers, whereas the buyers are willing to pay Rs 75 for each umbrella. So they would get some consumer’s surplus.

(iii) Both qualities are produced. In this case, competition ensures that the price will be Rs 65. The average quality available must, therefore, have a value to the consumer of at least Rs 65. This means that we must have

The lowest value of q that satisfies this inequality is q = 2/3. This means that if 2/3 of the suppliers sell high-quality umbrellas, the consumers are just willing to pay Rs 65 for an umbrella, for then the weighted average of 75 and 45 just becomes equal to 65; and if q > 3, then this average would be greater than 65 and the consumers would be willing to pay more than Rs 65 as price, and so now they would obtain some consumers’ surplus. It may be noted that if q < 3 , the buyers will be willing to pay less than Rs 65, and then no umbrella will be supplied since sellers will not be able to cover their costs. It may be noted also that as q → 0, p→ Rs 45.

Determination of the Ratio of High-Quality Umbrellas:

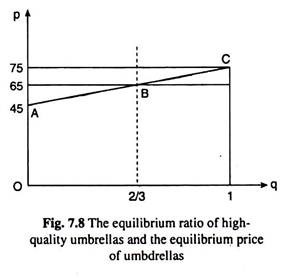
The determination of the equilibrium ratio of high-quality umbrellas may be done with the help of Fig. 7.8. Here the horizontal axis measures the fraction of high-quality producers, viz., q, and the vertical axis measures the price p that the consumers are willing to pay for an umbrella if the fraction of high-quality producers is q.

Producers are willing to supply either quality of umbrella at a price of Rs 65 so the supply conditions are shown by the horizontal line at Rs 65.

Here, the consumers are willing to purchase umbrellas only if 75 q + 45 (1 – q) ≥ 65. The boundary of this region is indicated by the dashed line. The equilibrium value of q is between 2/3 and 1, and the price at any value of q in this range is given by the BC segment of the line AC.

In this market, the equilibrium price is Rs 65, but the value of the average umbrella to a consumer may be anywhere between Rs 65 and Rs 75 depending on what actually the fraction of the high-quality producers would be between 2/3 and 1. Any value of q between 1 and 2/3 may become an equilibrium value.

However, all these equilibriums are not equivalent from the social point of view. The producers get zero producers’ surplus in all the equilibriums, since pure competition and constant marginal cost have been assumed. So here we have to examine consumers’ surplus only.

It is easy to see that the higher the average quality, the better-off the consumers are, for then they would be willing to pay a higher price than Rs 65.

The best equilibrium from the point of view of the consumers is the one in which only the high-quality goods are produced, for then they would be willing to pay the maximum price of the range 65-75 while they would actually pay Rs 65, thus obtaining the maximum possible consumer’s surplus.

Choosing the Quality:

We shall now slightly change the model and suppose that each producer can choose the quality of umbrella that he produces and that the cost of a high-quality umbrella is Rs 65 and that of a low-quality umbrella is Rs 60. All other things would remain the same as before. Let us see how the model would be different now.

Let us suppose that the fraction of high-quality producers is q, 0 < q < 1. Let us consider one of these producers. If he behaves as if under competition, and believes that his influence on the market price and the quality of the good is negligible, then he would always want to produce only low-quality umbrellas which are the more profitable product.

But since every producer will think in the same way, only low-quality umbrellas will be supplied in the market. However, the consumers will offer to pay only Rs 45 for a low-quality umbrella while its price will be Rs 65.

Therefore, no equilibrium can be achieved in such a situation with positive output. Only a zero-output equilibrium will reign the market. Therefore, the possibility of low-quality of production has destroyed the market for both qualities of the good.

Adverse Selection:

The phenomenon just described is an example of adverse selection. In the model we just examined, the low-quality items would crowd out the high-quality items because of the high cost of acquiring information. This problem of adverse selection may be so severe that it can completely destroy the market. We may consider a few other examples of adverse selection.

Let us consider first an example from the insurance industry. Let us suppose that an insurance company wants to offer insurance for bicycle theft. They do a market survey and find that the incidence of theft varies widely across communities.

In some areas there is a high probability that a bicycle will be stolen, and in some other areas, this probability is quite low. Let us suppose that the insurance company offers insurance based on the average rate of theft.

We shall see that the result of such an act on the part of the company would be its closure. We may easily see the reason— for, the people in the safe communities do not need much insurance anyway. They are not going to buy insurance, that too at an average rate. However, the people in the ‘unsafe’ communities with a high incidence of theft will want the insurance for they need it.

Now, the insurance claims will be made mostly by persons who live in the high-risk areas. Therefore, rates based on the average probability of theft will be applied to the buyers with a relatively high probability of theft. That is, the insurance company will not get an unbiased selection of customers.

Rather they would get a selection of customers, which is biased towards the high-risk category, i.e., the company will get an adverse selection of customers. Actually, the term adverse selection was first used in the insurance industry to describe the sort of problem just discussed.

It follows from the above analysis that in order to achieve the cost-revenue equality, the insurance company must base their rates on “worst”-case forecasts. But the consumers with a low risk of bicycle theft will be unwilling to purchase the resulting high-priced insurance.

A similar problem arises with health insurance. Here, the insurance companies, in order to break even, have to base their rates on the average incidence of health problems in the group of potential purchasers. Since these people are high-risk fellows, the resulting rates should be high, and the low-risk people will, therefore, be unwilling to buy the insurance policies.

However, everyone may be made better off if it is made compulsory for the people to buy insurance at a rate that reflects the average risk of the population.

For, then, the high-risk people will be better-off because they can purchase insurance at rates that are lower than the actual risk they face and the low-risk people will be better off, because now they can purchase at rates that are more favourable to them than the rates if only high-risk people purchased insurance.

Lastly, the insurance companies will be able to run their business profitably because now they would have no adverse selection problem.

This is a situation where the market equilibrium is dominated by a compulsory purchase plan. But it is quite surprising that compulsory purchase and restriction of choice that comes with it, can result in Pareto improvement. It should be remembered, however, that this paradoxical result is due to the externality between the low-risk and the high-risk people.

Also, there are social institutions that help to solve this market inefficiency. For example, employers offer health plans to their employees as a fringe benefit. The insurance company that implements the plans, can base its rates on the averages over the set of employees and is assured that all employees must participate in the programme, thus eliminating the problem of adverse selection.