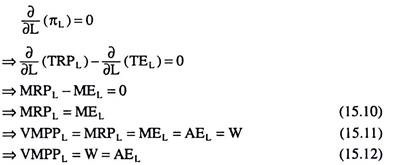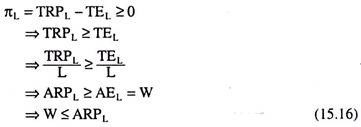The Marginal Productivity Theory (MPT) (With Diagram)

In this article we will discuss about the marginal productivity theory that discusses the demand for a variable factor of production.

Introduction Marginal Productivity Theory (MPT):

The leading exponents of the marginal productivity theory (MPT) are the neoclassical econo­mists J. B. Clark (1847-1938), P. H. Wicksteed (1844-1927) and J. G. Knut Wicksell (1851- 1926). This theory especially discusses the demand for a variable factor of production, and it does not throw any light at all on the supply of the inputs. That is why MPT is not considered as a complete theory of factor price determination.

The main contention of the MPT is that a variable input, say, labour, would get a price equal to its marginal product (MP). The increment in the total product of a firm that would be realised when an additional unit or the marginal unit of labour (the variable factor) is used, is known as the marginal physical product of labour (MPP_L or MP_L).

The Assumptions of the MPT:

The MPT is based on certain assumptions:

(i) The firm uses only one variable input, say, labour, along with some other fixed inputs, and there is no problem in using labour in variable quantities with the fixed inputs.

(ii) There exists perfect competition in both the factor (labour) and the product markets. That is, in the labour market, a large number of buyers and sellers are buying and selling a homogeneous labour input, and, in the product market, a large number of buyers and sellers are buying and selling a homogeneous product.

(iii) The quantity of labour (L) used by a firm is a continuous variable, i.e., it is possible to measure L in infinitesimally small units.

(iv) The law of variable proportions (LVP) operates in the field of labour employment, i.e., as the quantity of labour used (L) increases, MPP_L increases in the initial stages, and, after a certain point, as L increases, MPP_L diminishes.

(v) The goal of the firm is to obtain the maximum amount of profit, i.e., the firm would use the quantity of labour at which its profit would be maximum.

Measuring the Marginal Product:

Estimates of the marginal product (MP) of a variable input (labour) may be expressed in three different forms. These are:

(i) Marginal Physical Product of Labour (MPP_L or, Simply, MP_L):

The increment in the total physical product of labour (TPP_L or TP_L) of the firm that is obtained when an additional (or the marginal) unit of labour has been used is known as the marginal physical product of labour (MPP_L or MP_L).

According to this definition, we shall obtain the MPP_L when the quantity of labour used is n units if we subtract TPP_L at (n – 1) units of labour from the TPP_L at n units of labour. We may write, therefore,

[MPP_L] at L = n units = [TPP_L] at L = n units – [TPP_L] at L = n- 1 units                             (15.1)

(ii) Value of Marginal Physical Product of Labour (VMPP_L):

If we multiply MPP_L by the price of the product (p), we obtain the value of marginal physi­cal product of labour (VMPP_L or VMP_L).

Therefore, we may write:

VMPP_L = MPP_L x p                                                   (15.2)

Estimates of VMPP_L are obtained in units of money.

(iii) Marginal Revenue Product of Labour (MRP_L):

First, let us note that the revenue of the firm obtained by selling the product of the firm that is produced by a particular quantity of labour, say, L = n units, is called the total revenue product of labour (TRP_L) at L = n units.

Now, the marginal revenue product of labour (MRP_L) is defined as the increment in TRP_L obtained when an additional (or the marginal) unit of labour has been used.

Therefore, We may Write:

[MRP_L]_L = n units = [TRP_L]_L = n units ^_ [TRP_L]_L = n- 1 units                                       (15.3)

Obviously, the estimates of MRP_L are also obtained in terms of money.

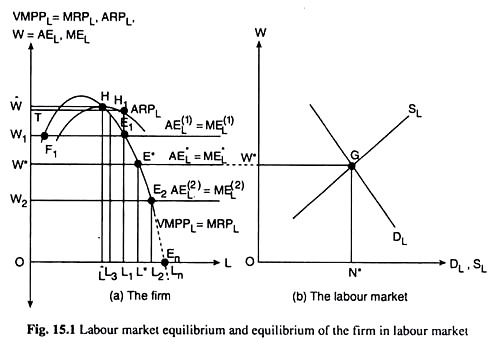
The VMPP_L and the MRP_L Curves:

In Fig. 15.1(a), the VMPP_L = MRP_L curve is the VMPP_L curve and, at the same time, it is the MRP_L curve. These two curves would be obtained as the same curve, because the assumption of perfect competition in the product market would give us VMPP_L = MRP_L at any L.

This we may prove in the following way:

According to the definitions, at any L and at the corresponding quantity of output (Q) produced and sold, we obtain

 

 

 

 

 

 

 

 

In Fig. 15.1(a), the shape of the VMPP_L = MRP_L curve has been like an inverted-U, be­cause, the MPP_L curve is like an inverted-U owing to the law of variable proportions and VMPP_L is nothing but MPP_L x P where P is a constant.

The ARP_L Curve:

In Fig. 15.1(a), the average curve associated with the marginal MRP_L curve is the Average Revenue Product of Labour (ARP_L) curve, From this ARP_L curve, we may obtain TRP ARP_L = TRP_L/L at any L. The shape of the ARP_L curve is also like an inverted-U owing to such a shape of the MRP_L curve. The MRP_L curve, while sloping downwards, would intersect the ARP, curve at its maximum point.

These features are obtained from the average-marginal relation. The ARP_L curve has been inserted in Fig. 15.1, because, this curve would help us to know the cut-off rate of wage, beyond which, if W rises, the firm would shut down its production.

The AE_L and ME_L Curves:

In MPT, it has been assumed that there is perfect competition also in the labour (factor) market.

Because of this assumption, the firm may buy any quantity of labour it requires at a constant rate of wage (W) which has been determined in the market, and that is why we obtain at any L:

W = AE_L = ME_L = constant                                  (15.6)

where W = the rate of wage = constant

AE_L = average expense for labour = W

and ME_L = marginal expense for labour

From (15.6), we obtain that the AE_L = ME_L curve of the firm is a horizontal straight line at the level of W. In Fig. 15.1, firm’s AE_L = ME_L curve is AE⁽¹⁾_L = ME⁽¹⁾_L, when W = W₁.

Conditions for the Equilibrium Quantity of Labour to be Purchased and used by the Firm:

In MPT, it is assumed that the goal of the firm is to maximise profit. Therefore, at the equilib­rium point, the firm would buy such a quantity of labour that would enable it to maximise the level of profit.

Now, by definition, the profit (π) of the firm, at any L, is:

π = TRP_L-TE_L-TFC                                         (15.7)

where TRP_L = total revenue product of labour,

TE_L = total expense for labour = total variable cost of the firm (TVC) (since labour is the only variable input)

TFC = total fixed cost, i.e., the total cost of the firm for the fixed inputs = constant. Since TFC = constant in (15.7), 71 would be maximum when TRP_L – TE_L is maximum.

Let us suppose:

π_L = TRP_L-TE_L                                            (15.8)

=>π = π_L-TFC [from (15.7)]                 (15.9)

Now, since TRP_L and TE_L are both functions of L in (15.8), π_L is also a function of L. There­fore, π_L has to be maximised w.r.t. L.

The first order condition (FOC), or the necessary condi­tion, for the maximum π_L, and, therefore, for maximum π, is: 

The first order conditions (15.10) and (15.12) give us that the profit-maximising quantity of labour for the firm would be obtained at the point of intersection between its MRP_L and ME_L curves or between its VMPP_L and AE_L curves.

These two points would be the same since VMPP_L = MRP_L, and AE_L= ME_L = W. Again, (15.12) also gives us that the firm would buy that quantity of labour at which the VMPP_L and the rate of wage would be equal. It may be remem­bered here that the VMPP_L = W, i.e., the labour would get a rate of wage equal to the value of its marginal physical product, is the main contention of the MPT.

Now, the second order condition (SOC) or the sufficient condition for the maximisation of π_L (and also of π) is:

What we obtain from (15.13) is that the slope of the MRP_L (= VMPP_L) curve should be less than the slope of the ME_L curve at the point of maximum profit—this is the sufficient condition.

Since the ME_L curve here is a horizontal straight line (slope = 0), FOC and SOC, i.e., (15.10) and (15.13) imply that, at the point of maximum profit, i.e., at the point of intersection between the MRP_L and ME_L curves, the slope of the MRP_L curve would be negative, i.e., this curve would be sloping downward towards right. That is,

∂/∂L (MRP_L) <0                                                                           (15.14)

Economic Interpretation of the First Order and Second Order Conditions for Maximum Profit:

We may give the economic interpretation of the FOC and the SOC, (15.10) and (15.13), in the following way:

Let us suppose that, in Fig. 15.1, the rate of wage (W) that has been determined in the labour market is W = W₁. Now, at any L, for example, at L = L₃, the profit of the firm obtained from the marginal unit of labour (i.e., the marginal profit) would be positive if we have MRP_L > ME_L = AE_L = W = constant.

For here the revenue product (i.e., revenue) obtained from the use of the marginal unit of labour is greater than the expense for this labour unit.

Now, if the profit from the marginal labour unit is positive, then the profit-maximising firm would be increasing the quantity of labour (L) to be used by it. And as L increases, the MRP_L may rise and then fall (because of its shape of an inverted-U), and eventually it would fall to the level of ME_L = constant, as we have obtained at the point E, in Fig. 15.1(a).

The firm would not increase L beyond this point (E,) because then its MRP_L would fall below the level of ME_L, i.e., it would have MRP_L < ME_L, and in that case, the firm would suffer loss on the marginal unit (its mar­ginal profit will be negative). At the point E₁, the FOC and SOC, (15.10) and (15.13), have been satisfied, since E₁ is the point of intersection of the MRP_L and ME_L curves and, at E₁, the MRP_L curve is negatively sloped.

We have to remember here that at the MRP_L = ME_L point like F₁, the firm’s profit would not be maximum, because if L increases beyond this point, the firm would have MRP_L > ME_L, and a positive marginal profit, which implies that it still has a scope of increasing its total profit by increasing L.

So, at the point like F₁, profit cannot be maximum. The firm would be increasing L in its quest for maximum profit till its MRP_L comes down to the level of ME_L at the point E₁. It may be observed that at the MRP_L = ME_L point F₁, the FOC has been satisfied but the SOC has not been satisfied because at F₁, the MRP_L curve is upward sloping—it is not downward sloping as required by the SOC.

A Third Condition—π_L ≥ 0:

We have obtained above the FOC and SOC, (15.10) and (15.13), for maximisation of π_L (and of π). Mathematically, we would have the maximum π_L (and n) if these two conditions are satis­fied. However, calculus does not ensure that the maximum π_L would not be negative. On the contrary, at some values of W, the maximum π_L may very well be negative.

Let us see its implications. We have π_L < 0 ⇒ TRP_L < TE_L [eq. (15.8)]. That is, if π_L < 0, then the total revenue product of labour (which is total revenue as a function of L) would be less than the total expense for labour, which means the firm would have to borrow to pay the (TE_L – TRP_L) portion of its labour expenses, and over and above this, the firm would have to borrow to meet its total fixed cost (TFC) obligations.

Therefore, in such an eventuality (π_L < 0), the total amount of loss that the firm would have to bear would be TE_L – TRP_L + TFC. Now, if the firm shuts down its production in this case, then the amount of labour employment (L) would come down to zero (L = 0) and the firm would not have to borrow anything to pay for its labour cost (we would have TRP_L = 0, TE_L = 0 and π_L = 0).

In this case, the firm’s loss would be equal to its TFC only. This is the minimum amount of loss that the firm would have to bear under the circumstances. That is, what we have obtained is that, if π_L < 0, then the firm’s labour employment (and output) would have to be made equal to zero. Only then its loss would be minimised (= TFC) and (negative) profit maximised (= – TFC).

On the other hand, if the firm has k_l > 0, then there may be two different possibilities. First, the firm may have π_L > TFC > 0. In that case, its k (= π_L – TFC) may be positive (k > 0) [eq. (15.9)] and the firm would certainly continue its output production. In the second case, the firm may have 0 < π_L < TFC.

In this case, the firm’s K would be negative (π < 0); but it would employ labour and continue its production. For here, the firm would be able to pay for a portion of its TFC with the help of its positive π_L, i.e., with the positive amount of (TRP_L – TE_L).

The firm’s loss in this case would amount to TFC – π_L. But the loss would increase and become equal to TFC if the firm discontinues production. In other words, in this case, the firm will continue its operations, for, by doing this, it would be able to minimise the loss or maximise (negative) profit.

Lastly, if the firm has π_L = 0 ⇒ TRP_L = TE_L [eqn. (15.8)], then it would have π < 0, being equal to – TFC, i.e., it would be a losing concern. Here if the firm shuts down, then its loss would be equal to TFC. On the other hand, if it continues, then also its loss would be equal to TFC, for now all its TRP_L would have to be used to pay for the labour expenses (TRP_L = TE_L).

Therefore, if π_L = 0, the firm would be indifferent between continuing and discontinuing the production of its output, because, in both cases, it would suffer the same amount of loss.

However, since the loss to be suffered when production will continue is not more than that when production will discontinue, we may assume that the firm will prefer continuing with its production when π_L = 0. Or, we may put the same thing in a slightly differ­ent way. π_L = 0 is a cut-off point. If π_L ≥ 0, the firm will continue production and L will be positive; if π_L < 0, it will shut down its operations and L will be zero.

Therefore, along with the FOC and SOC, (15.10) and (15.13), we get a third condition for the firm’s profit-maximising or loss-minimising labour employment, which is

π_L ≥ 0 => π ≥ TFC [eq. (15.9)]                                                   (15.15)

Relevance of the ARP_L Curve to the Labour Demand Curve of the Firm:

Condition (15.15) gives us:

Therefore, condition (15.15) reduces to condition (15.16). This gives us that the firm’s demand for labour will be positive if the rate of wage (W) is less than or equal to labor’s average revenue product.

Now, conditions (15.10), (15.14) and (15.16) imply that the firm’s labour demand curve would be that segment of the downward sloping portion of its MRP_L = VMPP_L curve that starts from the maximum point of the ARP_L curve and lies below it.

Therefore, in Fig. 15.1(a), the segment HE₁E₂. . . of the MRP_L curve would be the firm’s labour demand curve. Condi­tions (15.10), (15.14) and (15.16) also imply that the firm would demand a positive quantity of labour and continue to produce its output, if the rate of wage lies between 0 and W, both ends inclusive, i.e., if 0 ≤ W ≤ ŵ. That is, this range of W corresponds to the whole length of the labour demand curve HE₁E₂ . .. . E_n.

Let us explain:

 

 

 

 

 

 

 

 

 

 

 

 

We may conclude, therefore, that an analysis of the factor demand side of the MPT gives us that the firm’s demand curve for the variable factor, labour, under perfect competition in the product market would be downward sloping to the right, giving us an inverse relation between W and L (labour demand).

It would be the segment of the down­ward sloping portion of the MRP_L curve that starts on and from the maximum point of the ARP_L curve and stretches up to the L-axis. Actually, the firm’s labour demand curve is obtained in the second stage of production which is considered to be the efficient stage.

Equality between W and VMPP_L:

We have seen in the above analysis that owing to the assumptions of the MPT (especially, assumptions (iii), (v) and (vi), the firm would demand at any particular price (W) that quantity of the variable factor (here labour) at which the MRP_L = VMPP_L would be equal to W.

For example, in Fig. 15.1, when W = W₁ and W = W₂, the firm’s demand for labour would be L = L₁ and L = L₂, respectively. Since W would be equal to VMPP_L at any (W, L) combination, labour would always obtain a price that would be equal to the value of its marginal physical product. The main proposition of the MPT is thus established.

Complete and Currently Accepted Version of Marginal Productivity Theory (MPT):

What is known as the neoclassical version of the marginal productivity theory. This theory is so named because it has shown that the input demand is based on the value of the marginal product of the input.

But as a theory of the determination of the input prices based on competition, this theory is considered to be incomplete because it has not analysed the supply side of an input and, therefore, it has not attempted at input price determination through the process of demand-supply interaction.

But we may easily do this job and give the MPT a complete shape. Of course, as we have already noted, inputs vary considerably in respect of the nature of their supply.

Let us first complete the demand side. The MPT has given us the labour demand curve of a firm. We may now have the aggregate demand curve for some homogeneous labour service by taking the horizontal summation of the individual firms’ demand curves. Since the individual curves are downward sloping, the aggregate curve will also be downward sloping like the curve D_L in Fig. 15.1(b).

Now, on the supply side let us suppose, for the time being, that the aggregate supply curve of labour, like most other supply curves, will be sloping upwards towards right like the curve S_L in Fig. 15.1(b). In the perfectly competitive labour market, the equilibrium rate of wage would be determined in the process of interaction between demand for labour and supply of labour.

In Fig. 15.1, this rate wage is W*. It has been obtained at the point of intersection, G, between the D_L and S_L curves. At this rate of wage, demand for labour (D_L) has been equal to supply of labour (S_L) both being equal to N*, and the market is in equilibrium. This equilibrium is a stable equilibrium.

For if W > W*, D_L would be less than S_L, and there would be an excess supply in the labour market. In this case, the workers would be willing to accept a lower W to be able to sell their (excess) labour, and W would be coming down till it becomes equal to W*.

On the other hand, if W < W*, there would be an excess demand for labour in the market. Now the firms would be willing to offer a higher W to obtain their required labour quantities. As a result, W would be increasing and excess demand falling, till W becomes equal to W*.

At W = W*, there would be neither any excess demand nor any excess supply of labour in the market, and none of the buyers and sellers of labour would remain dissatisfied. Therefore, now the market would be in equilibrium.

In the perfectly competitive labour market, the buyers of labour, or the firms, have to accept the rate of wage (here W*) that has been determined in the market and they would decide what quantity of labour to buy at this W.

In Fig. 15.1(a), the firm concerned would buy a quantity of labour equal to L* at W = W*. We have already noted that, in the MPT formulations, W would always be equal to VMPP_L whatever may be the firm’s (W, L) equilibrium combination on the MRP_L = VMPP_L curve.

We may verify in Fig. 15.1(a) that at the (W*, L*) combination, i.e., at W = W*, the firm would buy such a quantity of labour (L*) that we would have W = VMPP_L. That is, labour would get a price that would be equal to the value of its marginal product.