The Law of Variable Proportions (With Explanations)

Introduction to the Law of Variable Proportions:

A firm increases output in the short run by varying only variable inputs.

Thus, the firm’s production function becomes:

Q = f (L, K̅, O̅)

In this production function, inputs K and O are assumed to be constant.

Now for different values of labour (L), we get different values of output (Q). The relation between L and Q are usually expressed in terms of ‘total product’ (TP) of labour. In addition, this concept of production function gives us concepts of ‘average product’ (AP) and ‘marginal product’ (MP) or marginal physical product (MPP) or incremental product.

A firm increases its level of production in the short run by making changes in input- mix. Here we want to learn the returns to a variable input. Changes made in input-mix and their impact on output is studied under a celebrated law in economics the law of diminishing returns, or the law of variable proportions, or the law of non-proportional returns.

Statement of the Law:

This law states that if we go on increasing more and more of a variable input, the amount of other inputs held constant, the returns to the variable input become non-proportional:

It may first show increasing returns, then constant for a while, and, eventually, diminishing returns. In brief, as additional units of a variable input are added to a given amount of fixed input, ultimately, average and marginal products of the variable input will decline.

Before explaining the non-proportional returns to the variable input, we must know the meanings of TP, AP and MP.

(i) TP:

Different values of a variable input, given a specified amount of the fixed input, will give us different values of output during a given period of time. Total output is usually called the total product (TP).

(ii) AP:

The average product of an input is the total product divided by the number of variable input (here L) needed to produce this output. It is the output per unit of the input used. In symbols,

AP = TP/ L

AP curve initially rises, then reaches a maximum, and declines thereafter.

(iii) MP:

The marginal product is the change in total output resulting form a change in the use of variable input (here L). In other words, it is the addition to the total product consequent upon a change in the employment of input. Symbolically,

MP = ∆TP /∆L

Or, MP = TP (L) – TP (L – 1)

MP is thus the difference in total product of the L-th unit and the (L − 1)th unit of production.

Thus the returns to the variable input are non-proportional: we first obtain increasing stage where TP, AP and MP rise. Then we have diminishing stage where TP increases at a slower rate and AP and MP decline.

Ultimately, we have a negative stage when TP declines and MP becomes negative. These increasing, diminishing, and negative stages of production can be explained with the help of an arithmetical example and figure.

Table 3.1 suggests that as the number of labour employed increases from 1 to 4 along with some fixed inputs, TP increases at an increasing rate, and hence, AP and MP rise. This is because of the fact that as variable input increases, better utilization of the fixed inputs occurs, thereby causing TP to rise at an increasing rate. This stage is thus known as the stage of increasing returns, or Stage I.

Now if more labour is added, diminishing returns to this variable input will set in. Increase in the number of labour from 5 to 8 causes TP to rise but at a diminishing rate. As a result, AP and MP decline. This stage has been christened as the diminishing stage of production, or the Stage II.

Finally, total productivity of labour now tends to decline gradually because of the fixity of fixed inputs. In other words, more employment of labour along with the fixed inputs results in an optimum utilization of fixed inputs.

Once this stage of optimum utilization occurs, any increase in labour will cause its productivity to decline. Once the 9th unit of labour is employed, TP declines from 64 to 63 units. As a result, MP becomes negative. This stage is characterized as the negative stage, or the Stage III.

(iv) Graphical Treatment:

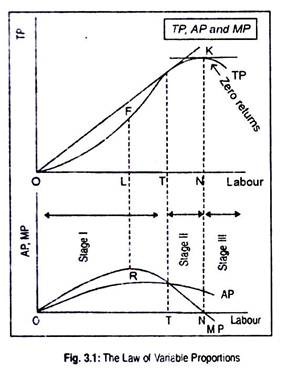
Now we use graph to explain the law of variable proportions. In Fig. 3.1, we measure units of the variable input (i.e., labour) on the horizontal axis, and TP, AP and MP on the vertical axis.

Consider first the TP curve. As labour is increased relative to the fixed inputs, TP curve rises rapidly, reaching its maximum slope at point F. Up to point F, TP rises at an increasing rate. Thereafter TP starts to decline. A typical TP curve thus shows that it rises initially slowly, then more rapidly and then more slowly again until it finally reaches a maximum and begins to decline.

Note that points below the TP curve are inefficient and points above the TP curve are unattainable. In this sense, TP curve has the similarity with the production possibility curve that separates the attainable as well as efficient output levels from those of unattainable levels of output.

Points on the TP curve are thus efficient. MP is the slope of the TP curve. Thus, the maximum slope of TP (i.e., point F) must correspond to the maximum on the MP (point R). Once the employment of labour crosses this point, TP increases at a diminishing rate. When OT unit of labour is employed, AP becomes maximum.

Beyond OT units of labour employed, TP continues to rise, of course at a diminishing rate, and reaches maximum at point K. Here the slope of TP becomes zero since TP is constant and, hence, MP becomes zero (corresponding to ON volume of labour employed). Beyond ON, if labour is employed, TP will decline and MP will become negative.

The relations among TP, AP and MP are used to define three stages of production:

Stage I is known as the stage of increasing returns where TP increases at an increasing rate and, hence, AP and MP rise. However, MP exceeds AP throughout this stage.

Stage II is called the diminishing stage since both AP and MP decline but are positive. This is the most crucial stage as far as the decision to produce is concerned.

Stage III is called the stage of negative returns where TP declines and MP becomes negative.

The above discussion will help us to show (i) the relationship between AP and MP, and (ii) the three stages of production in a nutshell form.

First, the relationship between AP and MP:

I. If MP > AP, AP will rise as labour increases.

II. If MP < AP, AP will decline as labour increases, and when MP = AP, then AP is at a maximum.

Now, the nature of three stages of production:

I. Stage I: MP > 0, AP is rising. Thus, MP > AP — increasing stage;

II. Stage II. MP > 0, but AP is falling. Thus, MP < AP, but TP is increasing because MP > 0 — diminishing stage.

III. Stage III: MP < 0 and TP is falling- negative stage.

Now a Pertinent Question:

Out of the three stages, where will the firm produce? It is argued that no rational profit-maximizing firm would produce either in stage I or in stage III. A sensible producer would always produce in stage II where both AP and MP of the variable input (here labour) are positive.

In stage I, though AP of the variable input increases, MP of the fixed input is negative. In this stage, fixed input is used in large proportion relative to the small doses of the variable input. There does not occur optimum utilization of the fixed input. As a result, its MP becomes negative.

Similarly, stage III is characterized by negative marginal returns of the variable input. Here the variable inputs are combined in large proportion with the fixed input. If the variable inputs are cost- free, even then the firm would not be dare enough to produce in this stage, though MP of the fixed input is positive.

As MP of the fixed input is negative in stage I and MP of the variable input is negative in stage III, a rational producer would never operate in th6se two stages. These two stages are known as “stages of economic absurdity” or “economic nonsense”.

Optimum utilization of both fixed and variable inputs takes place only in stage II. In other words, all the inputs are used in right or economical manner in this stage. That is why, in this stage, APs and MPs of both fixed and variable inputs are positive but diminishing. Production should occur in stage II.

Explanation of Increasing and Diminishing Returns to an Input:

In stage I, the fixed input is abundant relative to the variable input. This kind of defective input-mix results in an under-utilization of fixed inputs. As the number of variable inputs rises, fixed input tends to get combined with the variable inputs in an economical manner, thereby leading to an increase in productivity of the fixed inputs.

Probably, this is due to the fact that fixed inputs are generally indivisible. Indivisibility of the fixed inputs coupled with the rising numbers of variable inputs cause output to rise greatly due to the better utilization of the fixed inputs. Hence, indivisibility of fixed inputs is the first cause for increasing returns.

Secondly, as more and more variable inputs are employed, their efficiency tends to rise, because specialization or the so-called division of labour takes place. As a result, AP and MP of the variable inputs rise or average and marginal costs of variable inputs decline. Thus, the stage of increasing returns to a variable input is also known as the stage of diminishing cost.

Thereafter, a time comes when defective input combination gives place to optimum combination of fixed and variable inputs. Now, if more variable inputs are added, then, again, input combination becomes inefficient. Now, we have abundant variable inputs relative to indivisible fixed input.

As indivisible fixed input is used in wrong proportion with the abundant variable input, average and marginal returns must diminish. Secondly, there is a limit to specialization beyond which it cannot be increased. As a result, costs of production tend to rise. Thus the stage of diminishing returns may be called the stage of increasing cost.

Finally, one point must be pointed out here. It is argued that the law of increasing returns to a variable input or the law of diminishing returns to a variable input are not two different laws; they are just two stages of the law of non-proportional returns.

Applicability of the Law of Diminishing Returns:

The law of diminishing returns—the second stage of the law of non-proportional return— is applicable in agriculture as was believed by the classical economists. They, especially David Ricardo, argued that this law operates in agriculture due to the fixity of land—the natural resources. They also believed that the law of increasing returns is applicable to manufacturing.

But modern economists firmly believe that this law is even applicable to industrial production. For example, building construction, mining, fishing are other activities which are subject to diminishing returns in the ultimate analysis. Application of modern technology may postpone the appearance of the law of, diminishing returns for the time being. Ultimately, the law will set in. That is why this law is a universal one.