The following points highlight the two main objectives of a firm. The objectives are: 1. Maximization of Output Subject to a Given Cost 2. Minimization of Cost Subject to a Given Output.
Objective # 1. Maximization of Output Subject to a Given Cost:
Suppose, a firm purchases two inputs—labour and capital—with a given expenditure to produce a commodity. Further, let us assume that input prices are given. A firm operates efficiently if it maximizes output subject to input cost. To do this, it must select the proper input combination.
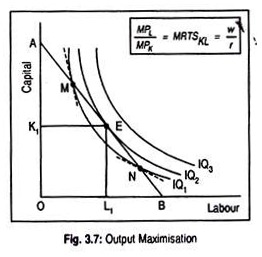
In Fig. 3.7, we have plotted an isoquant map labeled as IQ1, IQ2, etc., and an isocost line, AB. Given the cost constraint, the maximum amount of output that a firm can produce is IQ2. Such choice of output level, given the cost constraint, is determined by the tangency point (E) of isoquant (IQ2) and isocost line (AB). The optimum combination of inputs is, thus, OK1 of capital and OL1 of labour.
Let us see whether IQ2 level of output is maximum or not. Note that though IQ3 represents highest level of output and, hence, is desirable but that is unobtainable since available input combinations are limited to those lying on or below the isocost line AB. Given the cost constraint, a firm cannot go beyond the line AB.
ADVERTISEMENTS:
Further, IQ1 level of output—though obtainable given the cost constraint—does not indicate higher level of output.
A firm—even given the isocost line AB—can produce larger output if it stays on IQ2. Thus, point E (on IQ2 and isocost line AB) defines maximum producible amount of output given the cost constraint. In other words, a firm reaches equilibrium when the highest attainable isoquant becomes tangential to the given isocost line.
Alternatively, one can say that a firm reaches equilibrium when the slope of the isoquant becomes equal to the slope of the isocost line. In symbols,
ADVERTISEMENTS:
MRTSKL = MPL/MPK = w/r
This condition is known as the necessary condition, or mathematically, first-order condition. The condition for equilibrium is fulfilled at the point of tangency (i.e., point E). But at point M, the slope of the isoquant is greater than the slope of the isocost line. To understand this, we have drawn a tangent at point M on IQ1.
The tangent at point M, i.e., MRTSKL, is steeper than the tangent at point M on isocost line, AB. Thus, MRTSKL< w/r at point M. Point M is not the equilibrium point. By the same logic, N is also not an equilibrium point since at point N, MRTSKL< w/r.
In addition, there is another condition known as the sufficient condition, or mathematically, second-order condition. This condition requires that the isoquant must be convex to the origin at the point of equilibrium. This condition is again fulfilled at point E.
Objective # 2. Minimization of Cost Subject to a Given Output:
ADVERTISEMENTS:
An alternative to maximizing output for a cost constraint is the minimization of cost subject to a stipulated level of output. Under this least cost combination condition, a firm faces more than one isocost lines and only one isoquant to represent stipulated volume of output.
It is to be pointed out here that the conditions for equilibrium are the same. First- order condition states that MRTS equals input- price ratio. Second-order condition states that an isoquant must be convex to the origin. Because of the identical conditions for equilibrium of both the cases, these two yield identical results.
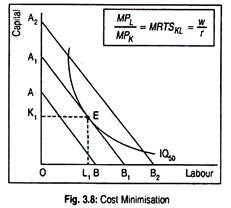
In Fig. 3.8, we have drawn three isocost lines represented by AB, A1B1 and A2B2. Higher isocost lines represent higher costs. The aim of a firm is the cost minimization. Here IQ50 represents the stipulated level of output. Our firm will not stay on isocost line AB since IQ50 output is not physically producible by an input combination available for this outlay.
If the firm incurs an expenditure represented by the isocost line A2B2, it will experience a larger cost to produce IQ50 level of output. Since the same level of output can be produced on a lower isocost line A1B1, why should the firm choose A2B2isocost line?
Thus, a firm will select an input combination of OK1 and OL1 of capital and labour, respectively, to produce IQ50 level of output. Note that at point E (i.e., where a given isoquant is tangent to lowest possible isocost line)
MRTSK for L = MPL/MPK = w/r
In addition to the fulfilment of this necessary condition or first-order condition for equilibrium (i.e., MRTSKL = w/r), we need another condition, known as sufficient condition or second-order condition. This condition states that the isoquant must be convex to the origin. Point E is the equilibrium point. Note that conditions for equilibrium are formally the same in both the cases.
This cost minimization principle is usually observed in the construction industry.