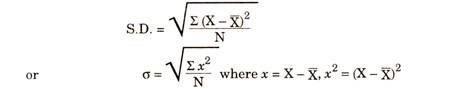The idea of Standard Deviation was first presented by Karl Pearson in 1893. This measure is widely used for studying dispersion.
Standard deviation does not suffer from those defects from which range, quartile range, and mean deviation suffer.
Standard Deviation is also called the Root-Mean Square Deviation, as it is the square root of the mean of the squared deviations from the actual mean.
Standard deviation is superior to other measures because of its merits showing the variability which is important for statistical data. The standard deviation enjoys many qualities of a. good measure of dispersion. In mean deviation we take the sum of deviations from actual mean after ignoring ± signs. In standard deviation, we get the same results without ignoring signs. In this case deviations from actual mean are squared, so every term is positive.
Where σ stands for Standard Deviation, ∑x2is the sum of the square of deviations measured from arithmetic mean, N is Number of terms. A point of difference is that mean deviation can be calculated from mean or median or mode but standard deviation is calculated only from mean.
Note: Deviation can be written with small x or dx
Coefficient of Variation Or Coefficient of Variability:
Like Coefficient of Standard Deviation, it is also a Relative Measure of Dispersion and was developed by Karl Pearson. If we want to check or compare the variability or consistency of two or more series, this measure is used. If Variability is more the consistency is less and if Variability is less then consistency is more.
“Coefficient of Variation is the percentage variation in mean, standard deviation being considered as the total variation in the mean.” —Prof. Karl Pearson
Comparison of Two Series:
Coefficients of C.V. are calculated for the series; the series is more consistent and less variable with smaller coefficient.