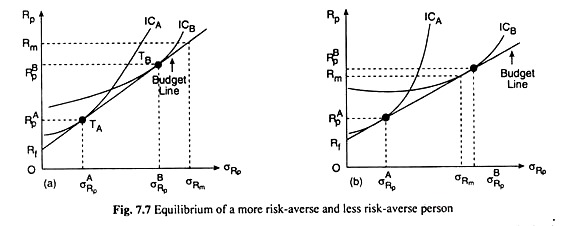
Let us suppose that the budget line of two persons are the same—this line is given in Fig. 7.7. Let us also suppose that one of these persons (A) is more risk-averse than the other (B). Therefore, the ICs of A would be steeper like ICA than those of B whose ICs would be like ICB.
Now, since A’s ICs are more steep at any σRp than B’s, A’s point of tangency or the equilibrium point would be obtained at a lower σRP as compared to B’s, i.e.,Other words, the more risk-averse person would prefer to have less of risk and return (at point Ta) than the less risk-averse person (at point TB), in Fig. 7.7(a).
In the above example, we have assumed that investor B has a lower risk-aversion than investor A. Now, if B has a sufficiently low level of risk-aversion, he might buy stocks on margin, i.e., he would even borrow money from a brokerage firm in order to invest more than he actually owns, in the stock market.
In effect, a person who buys stocks on margin holds a portfolio with more than 100 per cent of the portfolio’s value invested in stocks. This situation is illustrated in Fig. 7.7(b) which shows ICs for two investors. Investor A who is more risk-averse, invests about half of his funds in stocks.
ADVERTISEMENTS:
Investor B, however, has an IC that is relatively flat and tangent with the budget line at a point where the expected return on the portfolio (Rp) exceeds the expected return on the stock market (Rm).
In order to hold this portfolio, the investor must borrow money because he wants to invest more than 100 per cent of his wealth in the stock market. Thus, the investor may increase his expected return above that for the overall stock market, but at the cost of increased risk.