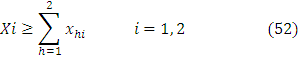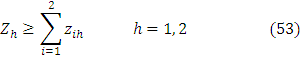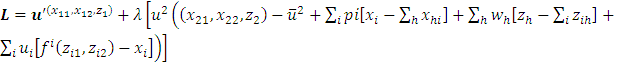Here is a term paper on ‘Welfare Economics’ for class 9, 10, 11 and 12. Find paragraphs, long and short term papers on ‘Welfare Economics’ especially written for school and college students.
Term Paper on Welfare Economics
Term Paper:
- Term Paper on the Introduction to Welfare Economics
- Term Paper on the Pareto Efficiency Conditions
- Term Paper on the Welfare Functions and the Pareto Criterion
- Term Paper on Market Failure
- Term Paper on the Instances of Market Failure
- Term Paper on the Coase Theorem
Term Paper # 1. Introduction to Welfare Economics:
ADVERTISEMENTS:
Welfare economics is deal with the resource allocation between individuals. It always tries to make at least one individual better off than no one worse off. In an economy, resources are used efficiently. Therefore, there is competition among individual to exchange the goods and increase welfare. Individual welfare is not different from the social welfare. The first best and second best theorem is explained in this section, Market failure and externality is last part but it has important implication on economy.
Pareto Efficient Resource Allocation:
In an economy, there is an allocation A and it is described as the use of resources in an economy. Such resources are the consumption bundles of the consumers. The labor in the economy supply inputs. The firms are using labor inputs and produce output.
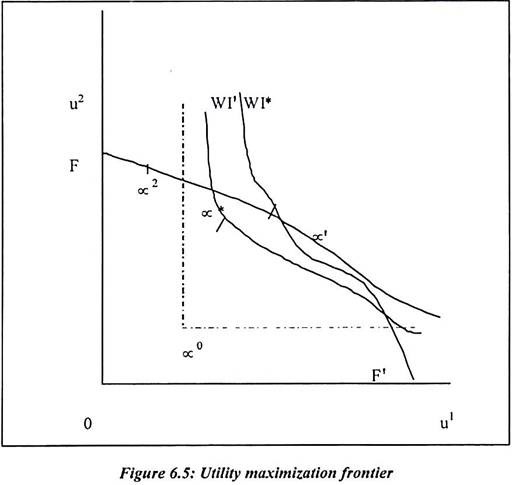
In Pareto efficient resource allocation, allocation A1 is Pareto superior to allocation A2. Suppose A1 generates at least as much utility for all individuals then A1 will get preferred. The diagram shows that all allocations which generate utility combinations (∝1, ∝2 and ∝*). Similarly in diagram, it is shown as the shaded area. They are the superior to the allocation and it generates ∝0. A Pareto efficient allocation explains that there is no other feasible allocation exists. Such allocation makes individual much better off and maximizes u’. The utility of individual 1 is subject to the constraints that is uh > u̅h where, h = 1,2………. H. Such constraints are imposed by technology and the endowments of the economy.
ADVERTISEMENTS:
An allocation is Pareto efficient if there is no feasible allocation. Such allocation is Pareto efficient allocation and it is superior to it. If we assume that there is variance in the minimum required utilities u̅h then it alters the Pareto efficient allocation. It is derived from the maximizing u’. A diagram shows that utility frontier FF’ which is derived by maximizing u’. Such utility frontier is subject to u2 > u̅2 for different values of u̅2.
The allocations are generating utility combinations on the utility frontier. Such allocations are as ∝2 or ∝* which are Pareto efficient. The allocations are generating points inside the frontier like ∝0 which are Pareto inefficient.
Paretian Value Judgments:
ADVERTISEMENTS:
In microeconomics, the concept of Pareto efficiency and Pareto superiority are widely used. It is important to realize that they are set of value judgments. Such judgments are not harmless at this point.
Process Independence:
The strong value judgment assumption explains the process of a particular allocation. It is achieved and it does not matter to show particular allocation. Suppose individual’s allocation mechanism produces the allocation which leaves him/her better off or worse off. Individual supply their own labor input and get better off. They get remuneration for supplying labor inputs. The centrally planned economy should allocate resources properly. The mechanism should allocate resources properly. The mechanism should not be their which will produce results itself.
Individualism:
Under the Paretian criteria the only aspect of an allocation which is relevant is its effect on the individuals in the society. Thus the output and input mixes of individual firm which is of no consequence for welfare purposes. It does not matter per se for example, whether a given output is produced in one large or many small firms whether the firm are privately or publicly owned or owned by foreigners.
The organization of production is relevant from welfare proposes only in so far as it affects the consumption or labor supplied for by individuals.
Non-Paternalism:
In the non-paternalism, it is assumed that individual is a best judge of their own welfare. But some individuals do not know their own preferences or do not respect the preference of other individuals. Each individual preference is diverse in nature. Each individual maximizes own preferences and get maximum satisfaction. Such maximization preferences are the basic subject matter of microeconomics.
But some preferences are bad and some are good preferences. The bad preferences are consumption of alcohol, tobacco chewing, smoking, drinking and driving etc. The good preferences are seeking health care, listen music, education and saving money etc. Every individual like to have good preferences but habit cannot be controlled. Sometimes preferences of individual become habits.
ADVERTISEMENTS:
Benevolence:
The Pareto efficient criteria are benevolent towards individuals. It increases the utility of one individual and it also lead to improvement in utility. Benevolence seems a very weak and therefore it is uncontroversial value judgment. Similarly it is not universally accepted concept. An increase in the well-being of a very rich individual, improvement is also possible. But at the same time, some individuals in the community can be malnourish or starving. Indian economy is growing economy but half of the children are malnourished.
Term Paper # 2. Pareto Efficiency Conditions:
In Pareto efficient conditions, we need to assume a simple economy. There is need to assume two consumers, two goods, two inputs, and two firms. The individual h has the following utility function.
ADVERTISEMENTS:
Such utility function is achieved after consumption of commodity 1 and 2. It is as follows
uh(Xh1,Xh2,Zh) whereis Xh1 consumption of commodity 1 and 2. We have assumed h is supply of an input.
The individual’s h initial endowments of the efficient inputs are denoted Z̅h. We assume that consumer has a non-satiation after consumption of Z̅h consumption bundles of commodities.
The marginal utility of consumption of bundle is positive and it is denoted as follows:
ADVERTISEMENTS:
The marginal utility of h of supplying more of input h is always negative. It is presented as:
In the Pareto efficient condition from produce the total output Xi. There are ith commodities produced by firms.
The production function of a firm is presented as follows:
ADVERTISEMENTS:
Where Zih is the quantity of input h, which is used in producing good i. We further states that the marginal product of input u in producing commodity i which is positive.
Therefore we have following equation:
In the above equation, we have taken simple derivative of production function. It is also possible that the total consumption of good i by individual will exceed the total output of firm i. The total use of input h by the firm may exceed the supply.
It is written as,
Above equation shows that each individual is maximizing utility and it is non-satiated. The marginal products are positive. It means that these materials balance requirement will bind as equalities in a Pareto efficient allocation.
In the strict inequalities, the input z1h could increase by increasing the output of commodity 1. It is permitting an increase in consumption by individual 1. Suppose equation 2 in above explanation is a strict inequality equation then the consumption of individual 1 will increase. It will increase without any increase in inputs. It must increase up to u’. In this condition, the feasible allocations must also satisfy the constraints.
The supply of input h cannot exceed individual h’s initial endowment where Z̅h ≥ Zh. The preferences are such that the inequality is always strict and the constraint never binds. Suppose, it is interpret Zh as labor then it is not implausible assumption. In the non-corner Pareto efficient allocations, we assume that there are two individuals who consume both goods and supply labor inputs to firm. The firms use the inputs of labor.
We can put this problem and solution in terms of Pareto efficient allocation as follows
We need to use equation 51, 52, 53 and develop Langrangean function for the Pareto efficiency problem. It is explained as follows:
We can take first order condition of the above function.
It is presented as follows:
Above equation explains Pareto efficient resource allocation condition. It is sufficient and necessary condition. Such condition is required for Pareto efficiency.
Efficiency Consumption:
For efficiency in consumption, we need to arrange equation 6 and 7.
Such equations are further explained as follows:
From the equation 55, it is clear that u11 = P1 and u21 = P2.
Presently, the equation 56 shows further derivation as follows:
For further explanation, we need to divide each of above equation for good 1 and good 2. It yields the equation 61.
The total output is efficiently allocated between two consumers. Such allocations must be ensured that they will equalize their marginal rate of substitution (MRSh21,) between two goods.
Now the MRSh21 measures the substitution rate, such rate is the rate at which h is willing to substitute commodity one for commodity 2. The MRSh21 measures h are marginal valuation of commodity one in terms of commodity 2. The consumption cannot be efficient if the individual have different marginal valuations of the goods. At the initial situation there is no Pareto efficient and equality of MRS. It is a necessary condition for a Pareto efficient allocation of goods among consumers.
Term Paper # 3. Welfare Functions and the Pareto Criterion:
In a welfare function, we need set of judgments. Such judgment provides complete, transitive and reflexive comparisons of allocations. It is a welfare preference ordering which is similar with individual preference ordering. Such a welfare preference ordering is further useful to rank all alternatives allocations. The welfare preference ordering is optimal allocation which has a feasible allocation. It is based on the above properties. Suppose the feasible allocation does not satisfies the above properties then the allocation is not exist. Therefore the existing allocation is ranked higher by welfare preference ordering.
A welfare preference ordering function is always used to rank all possible alternative allocations. The optimal allocation is a feasible allocation with the property. There is no other feasible allocation which is ranked higher by the welfare preference ordering. In the case of welfare preference ordering, it is continuous and such function can be conveniently represented by a Bergsonian social welfare function (swf). In this allocation, w (A) is defined as the allocation which maximizes w over the set of feasible allocations.
Now we can represent the social welfare function for two person economy. It is represented to reduce the complexity.
Such function is as follows:
From the above assumptions, we are free to make assumption of non-paternalistic value judgment. It means that individual is the best judge of his own welfare. He will choose best preference ordering. But now we need to change the above function slightly.
The above equation (65) can be written as:
Where, uh the hth is individual’s utility function. It represents her own preference ordering over her consumption bundles and labor supply. If it was felt that individuals were not the best judges of their own welfare then we could specify a swf. Such swf is the individuals own utility function which was replaced with welfare function. It is shown as gh(xh1, xh2, zh). Such function represents paternalistic views on the effect of allocations on individuals.
The benevolence value judgment implies that the partial derivatives of w with respect to uh or gh. They are positive values.
Therefore in conjunction with non-paternalism, benevolence implies the following function:
Pareto Optimality:
Pareto swf is a Bergson social welfare function. It is embodying the value judgment of individualism, non-paternalism and benevolence. A Pareto optimal allocation maximizes a Paretian swf and it is subject to the production and material balance constraints. A competitive equilibrium is optimal in the Paretian sense that no alternative feasible allocation of commodities can improve the lot of one agent without worsening the conditions of some other individual.
Equally important is that converse proposition that any given Pareto optimal allocation can be sustained by a competitive equilibrium. A prime achievement of welfare economics has been to establish conditions that are roughly speaking, necessary and sufficient’ for the validity of these conclusions in finite economies (i.e. economies in which the numbers of commodities and economic agents are finite). On the other hand, it is known that in non-finite economies, these propositions may fail even when the sufficient conditions of the finite case are met.
In following figure, the feasible utility combinations are those on or inside the utility frontier FF’. The Paretian swf w (u1, u2) gives rise to welfare indifference curves, such as wI1 wI*, which have slope.
The assumption of benevolence implies that the welfare indifference curves are negatively sloped. The higher indifference curves are corresponding to greater welfare. The utility combination ∝* on the utility frontier maximizes w over the set of feasible utility combinations. An allocation A* which generates the utility combinations ∝* is a Pareto optimal allocation. Different value judgments about the relative merits of the two individuals would be represented by a different welfare function. It would give rise to different welfare function and also it would give rise to different Pareto optimal resource allocations.
Compensated Principal:
The Hicks and Kaldor compensation test is an ingenious. The successful attempts have been made to extend the set of situations. But in such attempts, it is not practical. Therefore it can be compared without the need to specify value judgments, which are concerning the relative merits of individuals. It is required without the need to construct a Bergson swf. If we assume that vh(yh ℓ, ah ℓ) then such utility is individual h’s utility and he gets in situation ℓ, where yh ℓ. is the h’s income and ah ℓ is vector of attributes of the situation. Now it is depending on the context. An individual may set property rights regulating behavior.
It is defined implicitly as follows:
There are number of alternatives assumed in situation 1 and situation 2. We have assumed that situation 2 is better for individual 1 than situation 1. In the above equation cvh12 is assumed as positive. The amount individual is willing to pay for the change. Suppose, individual is worse off then cvh12 is negative. Individual much pay to accept the move from situation 1 to situation 2.
The Hicks-Kaldor compensation test recommends a move from situation 1 to situation 2. We can explain that compensation can be possible from situation 1 and situation 2. It is further stated as there are gainers in situation 1 and looser in situation 2. Suppose the gainers move from the situation 1 to situation 2, then gainers move can be compensate the losers still better off at same situation.
We can still recommend the move of the individual under different situation as follows:
We do not consider that individual 1 gains in his utility. Our major concern is that to examine the individual 1 which has utility gains and it is worth more than the utility loss to another. Every individual is best judge of their own utility. An individual always take decision to maximize his utility. Each individual is willing to pay money to get maximum utility. Sometimes a change in price level may force him to pay more. Therefore he will pay that much which can make him better off after the change as before.
Most of the studies of cost benefit analysis of public sector investment projects are based on aggregation of compensating variation. The projects of special economic zone are widely discussed for compensation to farmers. Here industrialists want to take more benefit from investment. They expect that government will provide various benefits for investment. But the farmers should not sacrifice for their livelihood.
There should be good compensation package to farmers. Similarly the land acquired for the projects such as nuclear plant, transport, ports have much environmental and economic value for farmers. The compensation need to think on the basis of harm to occupation and loss of income.
Criticism:
The theory is criticized on number of points.
Some criticisms are more valid and discussed in detail as follows:
1. Interpersonal Value Judgment:
If we assume that a change makes the rich better off and the poor worse off than it passes the compensation to rich people. This is because the rich could not compensate the poor and still be better off. Since some individual’s utilities have increased and other individual’s utilities have decreased. It is impossible to evaluate the change without making a judgment about the relative merits of the individuals and the existing distribution of income.
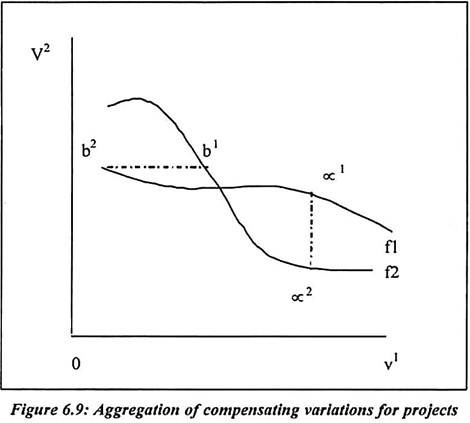
2. Change in Utility:
We have assumed that at initial situation generate the utility distribution ∝1. The new situation yields ∝2. In the new situation ∝2 it is possible to redistribute income from individual 1 to individual 2. It can be done to increase v2 and reduce v1. The curve f2 through ∝2. It is a utility feasibility curve which is showing the utility distributions. Such distribution can be achievable from situation 2 by transferring income between the individuals. In the diagram, f2 is passing through a point b2.
At this point, individual 2 has the same utility as in the initial situation and individual 1 has more utility. Therefore it is impossible for individual 1 to compensate individual 2. If there is move from situation 1 to situation 2 then individual 2 is better off. Therefore there is potential Pareto improvement and the compensation test is passed.
Now we can show the reverse argument. Suppose it is assumed that initial period the individual is at situation 2 where ∝2 is observed. There is move to situation 1 at ∝1 where individual 1 is worse off and individual 2 is better off. They are compete two different situations.
Suppose we apply the compensation principal then we need to examine the utility feasibility curve f1 through ∝1. It can be shown as the utility combination reachable from ∝1 by mean of transfers of income between the parties. In this case, it is possible to reach b1 where individual 1 has the same utility as it is observed in situation 2. At this point, individual 2 has greater utility. Therefore a move from situation 2 to situation 1 also passes the compensation test.
Such compensation test is known as the Scitovsky paradox. The compensation test may lead to cycles. It is mainly because compensation is not actually paid to individuals. We can show it with the help of equation and diagram. In equation form, we can define the compensation variation and its move from situation 2 to situation 1.
It is defined as follows:
Above compensation variation equation is only possible when cvh12 = ⎯ cvh21. It is possible for all individuals. We must be sure that there will be no paradox. Now suppose is the compensating variation for the move from situation 2 to situation 1 then it is also equivalent variation for the move from situation 1 to situation 2. The amount of money h must be paid in situation 1 to achieve the same utility as individual would get in situation 2.
Pareto Efficiency and Competitive Markets:
In the Pareto efficiency and competitive markets, the condition can be used to investigate for the particular situation. It means whether a particular institutional framework leads to an efficient allocation of resources. In this section, we will examine the circumstances in which the equilibrium resource allocation in a market economy is efficient.
Term Paper # 4. Market Failure:
We have seen that in competitive market economy, the Pareto efficient allocations are at equilibrium. We know that market may fail to allocate resources efficiently. When market fails, the role of government becomes very important. Now it is needed to understand how government solves the problem. There are different markets such as commodity, debt, equity, derivative and real estate.
The role of government in these markets is important. It is assumed that all market perform in particular way. But it is not true in long term. In each market, over the period of time the monopoly may get developed. Such markets may work in efficiently and it leads to misallocation of resources. There is an interdependence of market and economic agents exist in the market.
Most of the time, the public goods and its access to resources get affected. Such change is damaging the fundamental rights of the individual. Such changes and monopoly power also affect the property rights, information and transaction costs.
The Causes of Market Failure:
In any competitive market, individuals not only exchange the commodities but they have the right to use the commodities in particular way for particular length of time. For example, when any individual buy car, he is not just buying a physical asset but he is buying the rights to use that asset in certain specified way. Such rights are to derive on public highways, with certain speed, carry specific passenger if it used for as commercial vehicle with valid permit number and period. He has also the right to park at highway.
Every car owner has the right to park vehicle at specified amount at parking sites. The owner of the car can prevent other individuals from using the car without his consent. Similarly when any employer hires a worker then employer has certain right to direct the worker to perform certain activities such as activities need to perform within specified time which is a duty of the worker. Similarly the employer must provide the decent services at work place such as toilet, electricity, air, child care center for women.
Market is an institution which allows exchanging of goods. Such control is defined as the property right. Such property right is attached to each commodity when consumer buy commodity, the rights get transferred to individual. In the barter exchange, suppose the two goods are not equal for two consumers then inefficient allocation would exist. But such inefficient allocation can be corrected by rearranging consumption vector.
Such rearranging consumption vector will make at least one individual better off and no one worse off. There is possibility of mutually advantageous trade between two individuals. Suppose there is inefficiency exists then it is possible to exchange and make one individual better off than no one else worse off. But such in-efficiency explains the existence of potentially mutually advantages trades or profitable production decisions. Hence there are number of questions arises. Firstly, why a particular resource allocation mechanism is inefficient?
It can be repurchased as the question of why such advantageous or profitable exchanges or production decisions do not occur. Given that individuals would wish to make them-selves better off by trade or production, inefficiency can only persist. Firstly, individuals do not have sufficient control over commodities to affect profitable or advantageous exchanges and production. Secondly, transaction and information costs exceed the gains from trade. Thirdly, the individuals cannot agree on how to share the gains from their mutually advantageous exchange.
Inefficient Control: Imperfect Excludability and Non-Transferability:
The property right is defined as an individual’s control over commodities. The property right can be incomplete because of imperfect excludability or non-transferability.
Imperfect excludability emerges when effective control of a commodity is not conferred on a single individual but for a group of individual. Control over asset means the ability to determine who shall use it in what circumstances and how long. When a control of asset vested to a group then an individual wishes to acquire that control. In such circumstances, individual who wishes to acquire control enter into contract with the entire individual in the group. But it is difficult and costly. Therefore no individual can acquire exclusive control. Such assets are known as the common property resources.
The examples are common grazing land, ocean fishing, public parks and beaches, rivers and ground water and public transport. The control over asset is defined in terms of ability to exclude any individual. It means to determine who shall not use the commodity or asset. The term excludability has the first requirement is legality. The legal right to exclude must be supported by the ability to enforce that right. In some cases enforcement of the right to exclude is simple and inexpensive.
The owner of the house, car and land has the legal right to exclude others from using or occupying it. In case of land, farmer can put stone wall or compound to enforce his legal right on land. We often see the boards of owners on land. In case of cinema theaters, football ground must install box offices and gates, print tickets and employ staff to ensure that all who enjoy the entertainment must have tickets. At the same time, those who have paid for lower priced seats must occupy the low priced seats.
Those individuals want to prevent unauthorized use of their property then they may devote some resources for the purpose of detection, punishment of unauthorized uses etc. Such cost is known as exclusion cost. Such cost is depending on the legal and social framework of the economy and the technology. Sometimes person can use alternative strategies such as high intensive electric wire or theft alarms.
Such strategies could reduce the exclusion cost. It perfect excludability is not existing then potential advantage of trade or exchange will not take place. It will not help individual to acquire effective control or exclusive excludability.
A potential beneficial production may not occur if individuals making production decision which cannot exclude other individuals. A farmer has little incentive to plant crops if the law permits anybody to harvest the crops without the consent of farmers. Lack of exclusion may affect the benefits of output. This is because it reduces the gain of single individual and he may lose the incentive to the costs which is necessary to produce the extra output.
Non transferability arises when the legal right to exclude is vested in a single individual and exclusion costs are low. The owner of the asset does not have the unrestricted legal right to transfer use or ownership to just any individual by any condition or term. Lack of transferability may take the extreme form of a complete absence of the right to transfer any of the property right.
Such right may be associated with the good or asset of any terms to anybody. For example a squatters who occupy land of government without permissions but the squatter do not have right to provide land on rent or lease it. The squatter can exclude others from using it.
In terms of labor market, the individual own their labor and can sell labor for limited periods. But the law does not permit to transfer the permanent control over labor. By law, slavery is illegal. An exchange of manpower will be there when maximum or minimum price is fixed by law. The trade of commodities will take place in prescribed format. There are certain restrictions on which individuals may do the trade. But there are some restrictions under which individual do not trade.
But there are some restrictions which are most applicable. For example, youth aged less than 18 years cannot buy alcohol from licensed premises but youth can consume alcohol. A taxi or jeep cannot carry passengers unless they have license by the local transport authority. If they carry excess passengers then police will put fine or put them in jail for offence. Such activities are regularly practiced by police at different highways.
Information and Transaction Costs:
Exchange of commodities required information. The potential buyers and sellers must be known for exchange of commodities. The quality of goods or services to be exchanged and the property right must be checked. But getting all information is costly for individual. Individual has high searching cost to find trading partner. The quality checking and discovery of new innovation is costly affair.
There is cost of negotiation and specifying the terms of exchanges and of enforcing them. Such information and transaction costs may be high therefore the potentially advantageous contracts are not made or contract may be incomplete and leaving some potential gains unexploited.
Bargaining Problem:
Trade will occur when both parties will bargain and agree to sign contract. Such contract is mutually advantageous for trade. But if the gains are not positive then trading parties will get fail to bargain. Sometimes the bargains are very costly. Both parties fight for maximum gain and they cannot come at the common benefits. It is known if the contract is not signed then alternative possibilities are available. When both parties can find multiple contracts, the bargaining will fail. The exchange will take place when both parties will be better off. Suppose the trade is taking place at fixed level in the market then there is no scope for bargaining.
It is natural that if both get advantage after trade then trade will take place. But at the same time, if someone is getting worse off after trade off then they will not sign a contract. In a competitive economy, if one price prevails in the market then no buyer and seller will bargain. There is also no scope for bargaining. Here no buyer will play the price which is above the market price. Similarly no seller will sale above the market price. This is because no buyer will buy from seller. Both buyer and seller know the prevailing price exist in the competitive market.
Term Paper # 5. Instances of Market Failure:
There are different examples of market failure. Suppose the market is imperfect and it does not allow the parties to maximize their gains, then government efforts are must. Such efforts increase the efficiency in market. Before going in detail, we need to understand the example of monopoly and market inefficiency.
Monopoly:
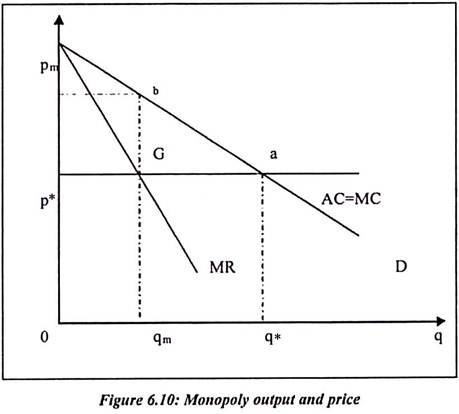
The monopoly form of market is itself based on profit maximization principal. In monopoly type market, the marginal revenue is equal to marginal cost. We can show it in the following diagram. In the diagram, gm and pm are the monopoly output and price points. Suppose consumer is paying pm price for commodity purchased then such situation is Pareto inefficient. The monopoly firm has marginal cost which is MC, where MR = MC and AC = MC.
But consumer is paying price pm which is greater than MC. Suppose consumer is paying less than pm but more than MC for the additional unit then he is continued to pay pmqm . At this point both producer and consumer are better off. At this point monopoly firm increases the profit from output. Consumer also gets the extra consumption at a price. It is less than the actual value to the consumer.
At this point, Pareto efficiency is achieved. This is because consumer is willingness to pay for unit. In the diagram, it is measured by the height of the demand curve. Such demand curve is equal to the cost of extra unit.
In the diagram q*is an output which shows demand curve which cuts the marginal cost curve. The monopoly price and output are inefficient. There are potential gains to consumers and monopolist of output which is increased from qm to the level of q*.
Now consumer and monopoly firm can sign a contract such contract lead to efficient output. Now the monopolist is agree to sell output q* at a price p*. Such price is equal to marginal cost. Now profit of the monopoly firm would fall up to (pm ⎯ p*) qm. Consumer pays lump sum to monopoly firm. Both can be better off and gain can be received. Such effect is measured by the area pmbap*. This area exceeds the (pm ⎯ p*).qm by G. The gains are available for division between the monopolist and consumers.
In figure 6.10, the marginal cost of higher for the monopolist. It is because a consumer and a producer fail to bargain and get mutual satisfaction. They may not agree to division of the gain from the increase in output. There is high cost associated with locating and organizing consumers. They may not able to agree on how the burden of the lump sum payment should get shared. Sometimes it is difficult to prevent consumers who do not contribute to the lump sum payment from enjoying the benefits from the contract with the monopolists.
Therefore monopolists may be forced to make individual contracts with consumers. Sometimes the monopolist cannot prevent resale at this point; he will set the same price in each contract. Such situation is called as the normal inefficient monopoly situation. It is point where demand curve is downward slopping where MR = MC. Consumer will treat prices as a parameter. An individual consumer cannot follow the monopolist at a lower price. This is because monopolist has no ability to prevent resale.
Externality:
An externality means some of variables affect on one person decision takers utility or profit. Such utility or profit is under the control of another decision taker. Here we can give example of the brewery located downstream of chemical work. Chemical work pumps effluent into the stream where it will pollute the water. Such effluent into the stream will affect on the output of wine. Wine production is depends on its choice of output level. Such input combinations and the amount of effluent has to be removed from the water. Such water can be used in beer production.
Now eternality is detrimental but in other causes there may be beneficial externalities. Now we take example of bee keeper which is located next to an apple grower. The bees will cross pollinate the apple trees; it is benefiting the orchard owner and feed off the apple blossom. Now it is benefitting to the bee keeper.
Such example is known as externality. We saw that beekeepers output of honey is depending on the number of apple trees. The output of apple is depending on the number of beehives. We can see that there is producer-producer, consumer-consumer externalities. But there is producer-consumer and consumer-producers externalities are also exist.
Negative externalities lead to inefficiency in production. This is because chemical factory will set the level of output to maximize profit. Such factory will not take into account of the effects of the resulting pollution on the profits of the brewery. Now brewery may be willing to pay the chemical work to reduce the amount of effluent. Such pay the chemical work to reduce the amount of effluent. Such reduction in effluent reduces the profit of firm.
Therefore the firms output of chemicals and the effluents are produced in fixed proportion. It is a reduction in effluent therefore it requires a reduction in output of chemicals. Suppose the reduction in the brewery’s cost is above the reduction in the chemical factory’s profit. There are potential gains from trade. The initial level of effluent cannot have been efficient. But again it is depend on who take initiatives to do this.
Term Paper # 6. The Coase Theorem:
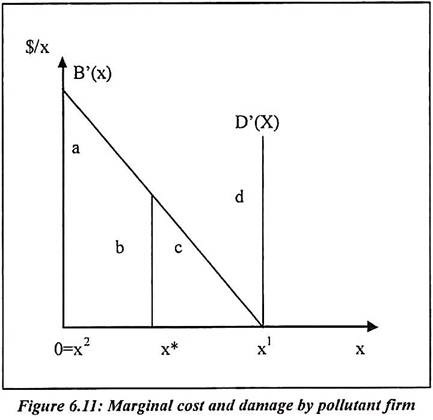
Now x is denoted as effluent of firm. Suppose chemical firm is producing output in a fixed proportion. The profit function of a firm is explained as B(x). The damage inflicted downstream because of the pollution which is D(x). In the diagram, the marginal benefit are B’(x) and marginal damage D’(x) from pollution is shown. If we assume that the profits of the two firms measured as the social value of their outputs then the effluent does not impose costs on any individual.
The profit of the two firms measures the social value of their output. The effluent level of pollution maximizes the total profit of the two firms. The efficient level of pollution maximizes the total profits of two firms.
The efficient level of pollution is x* which is satisfying the following condition:
There are two alternative legal situations that determine by which firm’s first set up in business on the streams:
(a) Permissive:
The chemical firm has legal right to discharge effluent into the stream. It control’s x and would choose a level of x1 here B’ = 0. The level of pollution is inefficiently large. This is because its effects on the brewery are ignored by the chemical firm.
(b) Restrictive:
Now we can explain that the chemical work has no legal right to discharge effluent and the brewery can prevent it by course order. In the diagram, it is shown that the brewery can control the level of pollution and chooses a level x2 = o. It is cost from the effluent which is minimized. A zero level of pollution is also inefficient. The brewery ignores the effect of its choice on the profit of the chemical works.
Now x1 and x2 are inefficient point in the diagram. This is because the potential gains from trade that is a contract between two firms to control the level of pollution.
If we assume the pessimistic view and firm reduces pollution from x1 to x* then the chemical firm’s profit is c. The reduction in the brewery cost is c + d. The contract which shows the brewery paid to the chemical firm is c + θd (0 < θ < 1). It is in exchange for a reduction in pollution from x1 to x*. It would achieve an efficient allocation of resources and make both firms better off. The brewery’s profit would increase by (c + d) ⎯ (c + θd) = (1 ⎯ θ)d. The chemical firm’s profit would be ⎯ c + (c + c + θd) = θd. The contract would generate a combined gain from trade of d.
From the legal point of view a contract by the chemical works paid the brewery θa + b in exchange for an increase in effluent from zero to x*. It would lead to an efficient level of pollution. It makes both parties better off. The payment to the brewery would more than compensate for the increase in cost b. The chemical works increase in profit a + b. It would more than cover the payment to the brewery. The contract would split and the gains from trade between the two firms.
In the Coase theorem, the bargaining can achieve an efficient allocation of resources whatever the initial assignment of property rights. Suppose in the diagram, the affected parties can contract with each other, then the externality will be internalized. The party who has the legal right to control the level of pollution will take into account of its effects on the other.
The initial assignment of rights does not affect the distribution of income. A permissive law can lead to efficient bargain and increase the polluter’s profit by θd and under a restrictive regime an efficient bargain increases it by θa. The externalities exist because of number of reasons.
In small number externality situations, there may be failure to agree on the division of the gains from a move to a more efficient allocation. In large number externality, the absence of contracting between polluters and victims may arise from any of the reasons. The free rider problem is likely to be important.
The general reductions in pollution always benefit victims in that area. Therefore individual victims will have a reduced incentive to contract individually with the polluter. A contract between the polluters and voluntary association of victims will have benefits. At such contract it is difficult to exclude those who do not pay. By law, it is not clear that the polluter has legal right to pollute or the victims have the legal right to protect from pollution.
Going in court and fighting for legal case is costly for both parties and individuals. The market for pollution is not competitive. A single polluter may have many victims and he may act like monopolist. Therefore there is interest in public intervention as a solution to the externality problem. Ideally government should take strict action on polluting firm. It is polluting land, air and water. The future consequences of pollution are affection on natural resources and people. Firms need to pay taxes and invest funds for environment sustainability.
But if there is corruption at government offices then controlling pollution is difficult task. Such model is more practical and widely used to arrive at the right conclusion. It is difficult to explain different examples and prove this theorem. But such example is important to understand the public intervention when negative externality exists.
In developing country like India, environment issues are widely discussed but government is not taking any action on polluting firm. Sometime the policy of moral suasion is most important to control pollution. Production, nature of technology, consumer preferences, land use are also important factor. We are not able to discuss all issues at this level. Common property resources and the government owned resources are exploited at great extent and there is no accountability for it.