Approaches of Saving and Investment Equality

Here we detail about the two main approaches of saving and investment equality.

1. Saving and Investment (Accounting Equality)—Static Approach:

Accounting equality between saving and investment is also called logical identity. Just as price is determined by demand and supply, so that, at each price, total amount sold is equal to total amount bought.

This happens on account of the fact that every transaction has two aspects (buying and selling on income and expenditure). In the same manner, total saving in the community is always equal to total investment at each level of income.

This identity of saving and investment holds true at all levels of income, regardless of the fact the savers and investors are two different sets of people.

Employment of labour at any time results in a certain amount of national output, which, in turn, results in the creation of national income. This national output consists of (i) consumption goods, (ii) investment goods (O = C + I). In the same way, national income is divided between consumption expenditure and saving (Y = C + S). But we know that by definition O = Y, therefore, C + I = C + S or I = S.

This equality between saving and investment can be expressed in another way also, for example, Keynes defined savings as the excess of income over consumption, i.e., S = Y – C. Further, investment is the name given to expenditures other than the consumption expenditures, it is nothing but income minus consumption or I = Y – C. Hence S = I (because both are = Y – C).

Importance of Accounting Equality:

It is useful to analyze the economic significance of the accounting equality of saving and investment.

The following arguments go to establish the importance of accounting equality:

(i) It helps us to explain the ‘paradox of thrift’, i.e., if all people living in the community try to save more, the total or aggregate saving will not rise. This identity reminds us that one man’s saving is another man’s reduced income, i.e., when one man saves more in the community, it means somebody else’s income is being lowered. Thus, the community’s attempt to save more without total increase in the income of the community would prove futile. This is the famous ‘paradox of thrift’.

(ii) The identity (S ≡ I) further points to the unfavourable results that flow from an attempt to save more than investment at a particular time. Both saving and investment, at a particular time are equal to Y – C, therefore, failure to spend more on the part of one man means the failure to earn more income on the part of another. This happens because a man is able to increase his saving only by curtailing his consumption, which leads to a decline in effective demand and hence income and employment. This is an important implication of S and I identity.

(iii) Saving and investment equality sheds more light on and paves the way for determinate or functional equality.

(iv) Further, the importance of saving-investment equality lies in the fact that it shows the condition that must be fulfilled in order to reach the equilibrium level of income.

(v) Moreover, the accounting equality of S and I has the richer implication that the factors of consumer and entrepreneurial behaviour must be fully analysed if the economy as a whole is in disequilibrium temporarily.

Saving and Investment Equality (Classical Position):

Keynes was not the first person to note the equality between saving and investment. Classical economists also talked of saving and investment being equal to each other. There are, however, important differences between the classicals and Keynes. Firstly, classicals believed that saving and investment equality is brought about by the rate of interest. When saving tends to exceed investment, the rate of interest falls to discourage savings on the one hand and encourage investment on the other.

Similarly, when investment exceeds saving, rate of interest rises to discourage investment and to increase saving. Thus, the disequilibrium between saving and investment is corrected by the rate of interest. Secondly, Classicals believed that this equality between saving and investment is always brought about at full employment income.

Both these propositions have been contradicted by Keynes. He held the opinion that the equality between saving and investment is brought about in the matter of saving and investment equality in the General Theory’—on apparent Keynes’ and the other ‘real Keynes’. We have seen that the economy is in equilibrium only when saving (in ex-post or realized sense) is equal to investment (in the ex-post or realized sense). This is what we may call real Keynes. But Keynes defined saving and investment in such a way that they are always equal identically. This is what we may call apparent Keynes.

This double meaning and dual approach of equality between saving and investment has been a source of great confusion for many writers and readers. The equality between saving and investment has been the cause of great debate and controversy on account of the differences of opinion on the definitions adopted by different economists of saving and investment. One source of confusion arose from the failure of the critics to realize that while saving and investment are always equal, they are not necessarily in equilibrium.

If the economy is in motion and the variables are always in a normal functional relationship to each other, then saving and investment are not only equal but may also be in equilibrium. But if the process of change involves lagged adjustment of certain variables, this will not be the case. For example, if there are consumption-expenditure-production lags, saving and investment through equal will not be in equilibrium. There can be no equilibrium position unless lags have worked through—once lags have been overcome or worked through, saving and investment are both equal and in equilibrium.

Another source of confusion arose because many of Keynes’ critics found it difficult to reconcile the equality of saving and investment with the undeniable fact that a part of the funds going into investment is financed from bank credit (new money) or from idle balances. How then, it was asked, could saving equal investment. In fact, Keynes himself is to be blamed for this confusion, for he did not clearly, discuss this issue.

However, this confusion need not arise if we just understand and appreciate the equality between saving and investment in two senses and distinguish between:

(i) The accounting equality of saving and investment,

(ii) Functional equality between saving and investment.

2. Saving and Investment (Functional Equality—Dynamic Approach):

The accounting equality of savings and investment (called identity) is not of much use for analytical purposes, partly because it throws no light on the causal factors that determine savings, investment, consumption and income and partly because it provides us no adjusting mechanism, by which such an equality is brought about. Since the equation is as true as the proposition that one plus one equals two, no mechanism of adjustment is involved.

To say that S = I leads nowhere, unless we know how such an identity is brought about. Since identity (S ≡ I) is not an explanation of the actual behaviour, this becomes a tool of static analysis. It is this static approach to S and I equality, which has necessitated the study of the actual and dynamic factors behind such an equality. Accounting equality merely represents the statistical result of the behaviour of national income or economic system during a given period. Functional equality, on the other hand, aims at studying the actual behaviour and the actual process of adjustment of saving and investment in the economy, as a whole. In other words, it aims at putting life into dead figures.

We have known clearly that the equality between saving and investment is brought about by the changes in the national income (and not by the rate of interest as stressed by the classicals). Let us see what happens when investment exceeds saving (by Rs. 20 crore) at a certain level of income (say Rs. 100 crore). This will increase national income through multiplier to such an extent that savings; out of the increased income would be equal to the investment (or the excess of investment, i.e., Rs. 20 crore).

Let us suppose that S = I when income (Y) is Rs. 100 crore. Let us suppose further that consumption (C) is Rs. 80 crore and investment (f) Rs. 20 crore, which is equal to saving (Rs. 20 crore). Suppose the multiple (K) = 2. Suppose further that investment increases by Rs. 20 crores and the total investment becomes equal to Rs. 40 crore (i.e., I > S by Rs. 20 crore).

This will generate a multiplier effect and give us according to ∆Y = K ∆ I. Rs. 40 crore [∆Y (40 crore) = ∆(2) x ∆I (20)]. Thus, the total national income will rise from Rs. 100 crore to Rs. 140 crore and out of this increased income of Rs. 140 crore, increased savings of Rs. 40 crore will flow (which are equal to increased investment of Rs. 40 crore). This will happen because the initial increase in investment (by Rs. 20 crore) will go to increase business activities in the capital goods industries, where more people will be employed.

Their incomes will increase leading to a rise in the demand for consumption goods. This will result in more income and employment in the consumption goods industries, leading to a multiplier or cumulative rise in the total national income of the community, making it possible for the increased savings to flow (which are equal to increased total investment i.e., Rs. 40 crore. It is in this sense we say that savings depend upon changes in income and not on changes in the rate of interest).

Therefore, by functional equality of saving and investment, we mean that both savers and investors, though they are quite different persons, having different motives, act and react to income changes in such a way that their desires to save and invest are expected to be reconciled in the very process of their actions and reactions.

Thus, we can easily conceive of a functional relationship between saving and national income on the one hand and investment and national income on the other. In this manner, saving schedule indicates various amounts of saving corresponding to different levels of national income and the investment schedule represents the various amounts of investment corresponding to different levels of national income.

However, there is some unique level (equilibrium level) of national income at which savings calculated from the saving schedule (in the schedule sense) are equal to investment calculated from the investment schedule (in the schedule sense). This is known as the functional equality of saving and investment.

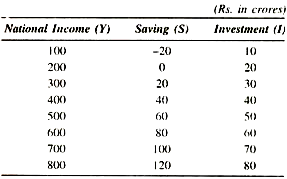
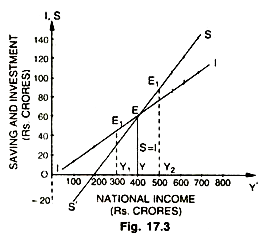
This is shown in the table and diagram given below:

Rs. 400 crore (OY) is that unique level of national income at which saving EY (Rs. 40 crore) are equal to investment EY (Rs. 40 crore), and which represents functional equality of S and I. This is also called equilibrium level of income, so that national income is neither rising nor falling (i.e., S – I = O). The economy is in disequilibrium in the diagram when the national income is Rs. 300 crore (OY₁) because investment is greater than saving by Rs. 10 crore. Therefore, income must rise from OY₁ to so that savings increase from Rs. 20 crore to Rs. 40 crore and are equal to investment. Similarly, at income of Rs. 500 crore (OY₂), savings (Rs. 60 crore) exceed investment (Rs. 50 crore) by Rs. 10 crore.

Therefore, income must fall from Rs. 500 crore (OY₂) to Rs. 400 crore (OY) so that savings are equal to investment at Rs. 40 crore at the equilibrium income level of Rs. 400 crore. This, however, does not mean that this income (OY) is a full employment equilibrium income or a full employment level of income, i.e., S and I are equal does not mean that there is necessarily full employment in the economy. It only means that S and I are, and can be, equal at less than full employment (popularly called underemployment equilibrium).

It is quite interesting to understand and to show the dynamic adjustment function. Let us see with the help of equations how the ultimate position of equilibrium is reached through time. Ignoring the inter-relation between periods of time, we can have a continuous (as distinguished from discrete) model such as:

The system is dynamic by virtue of Equation (c), which tells us the rate of change of income, dy/dt is a function of the difference between intended savings and intended investment, (I – S). At any moment the intended investment may exceed intended savings so that a higher level of income comes into existence and vice versa. Thus, income increases with excess intended investment and decreases with excess intended saving from one moment to another until the necessary condition of equilibrium is satisfied, as shown by Equation (d).

In other words, income must fluctuate, dy/dt > O, as long as there is a discrepancy between intended saving and intended investment at any moment, S I. It follows that dy/dt = 0, when S = I. Starting from t = 0, income set in motion by So Io can reach an equilibrium point via OY₀ → OY₁ → OY₂ → OY_n, according to Equation (c).