In this article we will discuss about the optimum theory of population. Also learn about characteristics and features of the theory.
The concept of optimum population is central to the study of the economics of population. Edwin Cannan and Carr Saunders are the chief exponents of the Optimum Theory of Population. In the decade of 1930s, Edwin Cannan and Carr Saunders worked out a new theory of population. It stated that growth of population is to be considered not in the context of food stock. Rather it is to be judged with reference to a country’s total volume of output.
In the words of Cannan, “At any given time there is what may be called a point of maximum return when the amount of labour is such that both an increase and decrease in it would diminish proportionate returns”. Thus, given the stock of capital, technology, natural resources, etc., at a given time, there exists in an economy that number of population just sufficient to exploit fully the resources of the economy and to obtain the highest possible output.
If actual population is more or less than the optimum, strains and stresses will develop leading to a fall in per capita income. In other words, if actual population exceeds or fall short of the optimum it would “diminish proportionate returns”. Optimum population can be defined as the size and structure of population which maximises the output (per head) of the economy and is thus most conducive to the betterment of the wealth and welfare of a society.
Features of the Optimum Theory of Population:
The main features of the theory are briefly summarised here:
1. Basis of the Study:
ADVERTISEMENTS:
The optimum theory seeks to establish a relation between the number of people of a country and its productive resources as it exists at a particular point of time. It has not studied the growth of population in the same manner as has been done by Malthus.
2. Meaning of Optimum Population:
The theory states that in every country there is a certain number of people or a certain size of population which may be treated as ‘optimum’ at a particular time. Population comes to the optimum level (or desirable level) when the per capita real income of a country reaches the maximum level, relative to the country’s existing productive resources and technology.
In other words, the population of a country becomes optimum when the country attains the highest level of productive efficiency with its existing stock of its resources and current technology, i.e., with its short-run production possibilities.
ADVERTISEMENTS:
The theory assumes a fixed stock of productive resources and a fixed framework of production techniques. It is obvious that the number of optimum population of a country would change with the change in productive resources and production techniques. So, the point of optimum is not a fixed one, but its keeps on changing.
3. Under-Population and Over-Population:
The theory further states that any deviation from the optimum point produces either under-population or over-population. A country is regarded as under-populated when an increase in population would cause an increase in the per capita real income of the people; on the other hand, a country said to be over-populated when an increase in population would cause a fall in the real per capita income. Thus, a fall in the real per capita income with an increase in the size of the population is to be treated as the symptom of overpopulation.
4. Measurement of Maladjustment in Population:
Dalton developed a formula to measure the degree of mal-adjustment in population (i.e., extent of under-population and over-population), which is as follows:
M = (A – O)/O
ADVERTISEMENTS:
In the formula, M stands for degree of mal-adjustment in population, A for actual population and O for optimum population. When M becomes zero, there is neither overpopulation nor under-population, i.e. the size of the population in optimum.
When M is equal to a positive number, that would indicate “overpopulation” and the positive number would itself indicate or measure the extent of over-population relative to the theoretical optimum. On the other hand, when M is equal to a negative number, there would be “under-population” and the negative number itself would measure the degree of under-population relative to the theoretical optimum.
Let us suppose that the actual population (A) of a country in a particular year is 20 crore and the optimum population (O) is estimated to be 15 crore in the same year. The value of M then will be positive, i.e., 1/3. It means that the country is over-populated to the extent of one-third of its estimated optimum population.
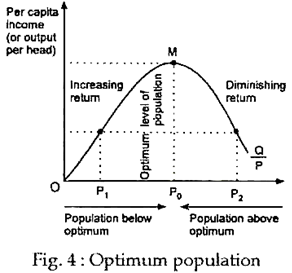
The concept of optimum population as explained can also be shown diagrammatically. The basic point to note is that if the size of a country’s population is too small in relation to its non-human resources, under-population exists; if it is too large, a country is said to be suffering from overpopulation. The concept of optimum population is based on the assumption that technology, trade and competitive conditions in the economy remain constant and only the size of the population varies.
Given these assumptions, then, as the size of a country’s population increases output will initially increase. But, eventually diminishing returns set in and as population grows further output per head falls. This point is illustrated in Fig. 4. Output per head is maximised as point M with population OP1.
Increase in population above OP0 causes output per head to fall and the difference P0 – P2, between actual population (P2) and optimum population (P0) is a measure of overpopulation, with OP2 giving a lower per capita income (OC) than population OP0. On the other hand, population OP1 is not sufficient to exploit natural resources and the returns to scale and, therefore, also corresponds to a lower per capita income (OC) than OP0. So, OP1 indicates that the country is under-populated.
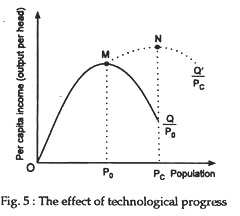
Two points are to be noted in this context. (1) Firstly, what is optimum (population) for one country may not be the same for another country. (2) Secondly, the optimum level is not static. This means that what is optimum today may not be optimum tomorrow. In fact, if we allow for improving technology or the discovery of new resources, then the optimum level of population will rise. The peak of the income in Fig. 4 will move to the right as Fig. 5 shows.
If we drop the assumption that technology is fixed, it may be possible for increased productivity through technological change to offset the effect of diminishing returns. In such a situation the optimum population may coincide with the actual population as population grows.
ADVERTISEMENTS:
In Fig.5 as population grows from OP0 to OPc technological change increases productivity per head, thus offsetting the effect of diminishing returns and shifting the most efficient, or optimum point from M to N, the optimum population being the same as the actual population OPc.
So, our prediction here is that, as the size of the population grows, there could be a succession of points such as M and N each giving a higher per capita income and, therefore, an improved standard of living.
Merits of the Optimum Theory of Population:
The optimum theory of population has some distinct merits:
1. Broader Perspective:
ADVERTISEMENTS:
The theory is more realistic and comprehensive as it discusses the population problem against the broader background of the total productive wealth of a country.
2. Need of Increase in Population in the Situation of Under-Population:
The theory justifies an increase in population in the situation of under-population; as such an increase would lead to a rise in per capita income of the people.
Defect of the Optimum Theory of Population:
But, the theory has some defects too:
1. Not a Growth Theory of Population:
The optimum theory is not a theory regarding the growth of population. It does not discuss how population grows in a country over time; it simply discusses the relation between the population and the productive resources of a country at a fixed point of time.
2. Static Theory:
ADVERTISEMENTS:
The concept of optimum population is a static one and hence is irrelevant and inapplicable to a dynamic world. The size of optimum population depends on certain factors which have been constantly changing. So, the optimum number must be changing constantly and because of that the optimum population of a country cannot be properly determined.
3. Abstract Concept:
The concept of optimum population is an abstract one as it does not refer to a particular number, but to a particular position.
Hence, difficulties would arise in measuring optimum population at a particular point of time.
4. No Practical Importance:
Owing to the above-mentioned limitations, the theory is “of extremely little practical interest” in framing economic policies relating to population, income, employment and growth. This is why modern writers have practically discarded the theory.
In fact, the concept of an optimum number of populations is vague. In a world, where technology is fast changing and new resources are being discovered constantly, optimum concept itself becomes dynamic. Given a situation in which actual population is equal to the optimum population, the invention of a new technology may make it overpopulated and the discovery of a new mine may convert it into an under-populated economy. Thus, in real life it is difficult correctly determine out an optimum number. Even if such a number can be found, that will be highly fluctuating from time to time.
Furthermore, when resources remain under-utilised, an increase in population, according to the theory, would bring about an increase in national output. But, it may do so after a lapse of time. For the people of a company will to attain working age and have to acquire necessary skill. By that time, the size of the population would have increased.