How to Calculate Frequency Distribution?

It is series that deals with discrete variables. It is the series in which data are presented in a way that exact measurement of units of the items or terms are shown clearly.

If we are to prepare discrete series from individual series or raw data, it is better to place values in ascending order, then against these variables we put tally bar for each item against the corresponding variable, then number of total tally bars is counted and a numerical number is put in 3rd column as frequency.

EXAMPLE:

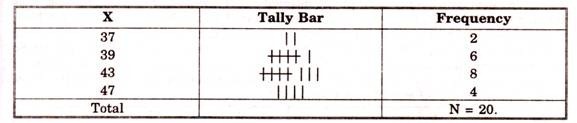
Weight of 20 students of a class is given as following. Prepare discrete frequency distribution (In kgs.) 37, 39, 43, 47, 39, 43, 37, 39, 43, 43, 39, 4 7. 43, 43, 39, 39, 43, 47, 47, 43.

Solution:

We put in ascending order first.

37, 37, 39, 39, 39, 39, 39, 39, 43, 43, 43, 43, 43, 43, 43, 43, 47, 47, 47, 47.

We find that there are only four variables i.e. 37, 39, 43, 47.

So taking these as variable X, we put tally bars and construct the table shown.

Continuous Series:

It is the series that deals with continuous variable. It is such a series in which items may or may not be exactly measured. They all are used within limits. Here even fractional values can be placed in corresponding class intervals. Here class intervals are taken instead of the variable and tally bars are put against these intervals. Then frequency is calculated from tally bars.

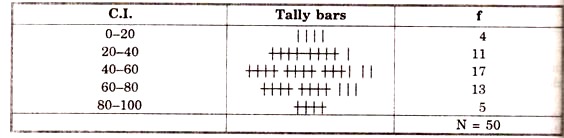
EXAMPLE. Marks of a class of 50 students are given as following.

Construct continuous series with intervals 0-20. 20-40…… 80- 100.

21, 3, 47, 42, 24, 0, 27, 59, 68, 37, 78, 11, 33, 79, 41, 29, 39, 54, 46, 82, 44, 30, 49, 51, 84, 54, 47, 51, 30, 56, 61, 66, 51, 32, 67, 71, 57, 50, 37, 61, 76, 81, 71, 58, 68, 87, 99, 77, 70.

Solution:

We take class intervals as 0-20, 20-40 ……. 80-100, put tally bars and count them and find f; N = ∑f

1. Exclusive Series:

Series such as 0-10, 10-20, 20-30……. is known as exclusive series. In such series upper limit of one interval is the lower limit of next interval. 10 are the upper limit of 0-10 but lower limit of next interval 10-20. Similarly 20 are upper limit of 10-20 but lower limit of 20-30.

In such series 0-9 limits will be included in interval 0-10 but 10-19 in 10-20. We find that 10 has been included in 10-20 and not in 0- 10. So upper limit of class interval does not contain the variable equal to that. A sample of exclusive series is shown in the table. Here items with magnitude 0-9 are 4, 10-19 are 6, 20- 29 are 16, 30-39 are 12 and 40-49 are 2.

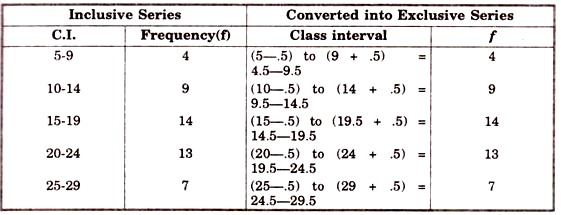
2. Inclusive Series:

In such series upper limit of one interval is not equal to lower limit of next interval. Series such as 5-9, 10-14, 15-19, 20-24…………….. is known as inclusive series.

To transfer this series into an exclusive one, we proceed as follows:

Difference between upper limit of one interval and lower limit of next interval is noted; then half of that difference is deducted from lower limit of every interval and the same is added to upper limit of every interval.

So in given example above, difference in the upper and lower limits of successive intervals is 1 ; Hence half of it i.e., 0.5 is subtracted and added to the lower and upper limit respectively of every interval and thus we get intervals as 4.5—9.5, 9.5—14.5, 14.5—19.5, 19.5—24.5 , which is called the exclusive series.

Problems in which we want to find the value of M, it is not necessary to do so as Mid Points of the inclusive as well as exclusive series remain the same, e.g. 10+14/2=12 and 9.5+14.5/2 = 12

3. Open End Intervals:

These are those intervals or classes, which either the lower limit of first interval or the upper limit of last interval or both of these, are not given. Here only an assumption about the length of these intervals is made according to the length of the interval nearest to these intervals.

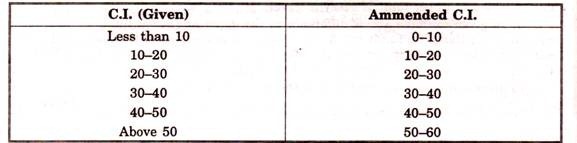
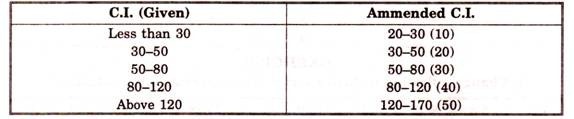
Let us suppose the given class intervals are ; Less than 10, 10-20, 20-30, 30-40, 40-50, more than 50 ; Then the desired class intervals i.e. 1st and last are 0-10 and 50-60 respectively ; as the length of intervals nearest to these two is also 10 i.e. in intervals 10-20 and 40-50. But if class intervals are not equal, then first interval should be taken equal to second and last equal to penultimate one. In some cases, some special methods are also applied. See table below.

In first case C.I. are equal i.e. 10, Therefore first and last intervals are also taken equal to 10.

In second case, intervals are in unequal, in such condition first C.I. is taken equal to second and last is equal to second last.

In third case, given intervals are 20, 30 and 40; hence first interval is taken as 10 and last as 50, to make a sequence of 10, 20, 30, 40 and 50.

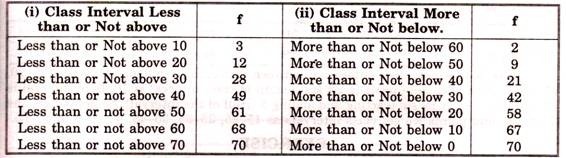
4. Cumulative Series:

In this type of series the frequency is not put against the interval corresponding to that one but is cumulated as shown in the tables. In the other table it has been converted into exclusive ones.

These series are of two types e.g.:

(i) Less than

(ii) More than

OR

(i) Not above,

(ii) Not below, as given below:

Conversion into Exclusive Series:

5. Mid Value Series:

These are then series where frequency is allotted against the mid points of the corresponding class intervals. When middle points are given, we convert it into exclusive series noting the difference between each midpoint, we get the length of each interval as follows.

Given.

Here as we note that difference between successive mid points is 10 (30-20, 40-30….). Now if middle point is 20 and length of class interval is 10, then interval is 15-25. This we get by subtracting and adding 5 (Half of the interval). So applying same to all the mid points we get class intervals as 15-25, 25-35, 35-45, 45-55 and 55-65.

6. Unequal Class interval Series:

These are the series which have unequal class intervals. We need not always to make them of equal intervals but some time it becomes necessary to do so as in case of computation of mode.

This can be under taken by either of the two methods:

(а) Combining or integrating the of intervals,

(b) Disintegrating the intervals.

(a) Combining the intervals:

If series is given as.

Here intervals are either of 10 or of 20, we combine some intervals to get all intervals of 20 each. So we get.

(b) Disintegrating the series:

If series is given as

Here it is impossible to get equal intervals of any magnitude by combining the given intervals. But if we take all class intervals of 5 each we get the class intervals and frequencies as below.