Investment Criteria for a Developing Economy (With Diagram)

In this article we will discuss about the various investment criteria’s for a developing economy.

The Incremental Capital-Output Ratio Criterion (ICOR):

Allocation of resources is one of the central problems faced by all economies. Establishing criteria for investment of a nation’s resources are crucially important for poor countries. One of the most traditional of the investment criteria uses the capital-output ratio as a key economic indicator.

In this view, investment should be made in those activities in which the greatest output per unit of investment will be forthcoming or—what is the same thing—the least investment per unit of output. Economic decision makers, private or public, would seek activities in which the capital-output ratio is lowest and concentrate their resources there.

In the 1930s and 1940s the Harrod-Domar model was becoming increasingly popular. It was thought that one could use the capital-output ratio as the basis for choice of investment project in an investment programme. If G = s/ where G is the growth rate and s the savings ratio and k the incremental capital-output ratio (ICOR), the lower the k, the higher the G. So the first approximation to a criterion for investment choice was a project’s ICOR.

These commonsense notions, however superficial they may prove to be on more detailed examination, have a secure place in the world of economic theory. The Harrod-Domar model focuses on the capital-output ratio as one of the two central parameters in determining the rate of economic growth. In this article, we discuss the statistical derivation of the ratio and its usefulness. Its possible shortcomings as an investment criterion, already alluded to, are of little practical interest unless superior alternative criteria are available.

We have already noted that the capital-output ratio is often used as an investment criterion and plays a key role in the Harrod-Domar model. For most purposes, we use the marginal or incremental capital-output ratio (ICOR) rather than the average (ACOR).

We want to know how much additional output is associated with a given addition to the capital stock, i.e., with a given amount of investment, or an additional amount of investment. Let us suppose that there is no difficulty in defining national production or capital formation. Is there than any problem in calculating the ICOR? The answer, as one might expect, is yes.

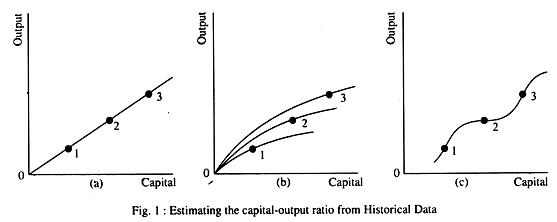
First, suppose we have three observations of capital and output, as in Fig. 1 (a). Is it possible, by drawing a line between them and extending it to the origin, to conclude that the ICOR is the same as the ACOR, and steady? It is not. To reach this conclusion is possible only if other things are equal.

If technology has been changing, as in Fig. 1 (b), the ACOR and the ICOR may each be steady, but widely different. Or, technology may remain unchanged, as in Fig. 1 (c), but with very different ICORs in each period and the same ACOR. The model assumes other things equal; in the real world, other things do change.

Second, should we take ICOR gross of depreciation or net? It evidently makes a considerable difference since, unless D or depreciation is very small

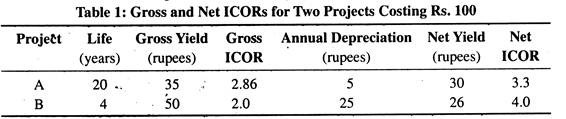
Assume there are two projects, each costing Rs. 100 but of very different lives- one lasting twenty years, the other four. Suppose that there is no ambiguity about what depreciation should be charged and that straight-line cost is the appropriate basis, physically as well as financially. Then as Table 1 shows, the gross ICORs favour project B, the net ICORs project A.

The answer to the question can be provided by adding a qualifying clause, “It depends”. Here, it depends on whether the capital structure is likely to be fairly stable or whether transformations in the structure of the economy are frequent.

With stability, it is sufficient to deal with net output, since depreciation allowances are not needed to shift capital to other sectors. If there is a large possibility that capital will be shifted into other industries, however, as transformation occurs, then gross production is the most relevant concept.

Another aspect of this distinction is raised by the question—whether one ought to consider the capital or the current cost of the capital input in choosing between two competing investments? The longer the life of the capital, the smaller the depreciation charge in any one year and the lower the capital cost, calculated gross. But this type of reasoning may lead to danger, since it favours long-lived capital.

A number of other significant questions are raised by depreciation. For one, there is no fixed scientific basis for calculating depreciation for a given capital asset. In most instances, depreciation is charged fairly uniformly through the life of the assets, either in a straight line or with constant percentage formula. Physically, however, some capital tends to wear out more rapidly at the end-part of its life than in the beginning.

It is possible, therefore, in a growing economy, to reinvest depreciation allowances from recent investments in new capital formation and rely on the greater productivity of the economy later when development has proceeded some distance to make good the physical exhaustion of capital.

Moreover, if an economy is consistently growing, straight-line depreciation will continuously provide more depreciation allowance than is needed to make good physical wearing out. But this is a simple property of geometric growth.

Third, there is the drastic oversimplification involved in comparing this year’s investment to this year’s increase in output. This is a helpful device but analytically unsatisfactory. Some additional reality can be introduced by a lagged model, in which inputs in period t lead to output in period t + 1 and inputs in period t + 1 yield their outputs in period t + 2.

Says C. P Kindleberger:

“When an economy undertakes all three types of investment— point-input, point-output; continuous-input, continuous-output; and point-input, continuous- output—the capital-output ratio that relates this year’s output to this year’s investment is evidently wide of the mark.”

In fact, in a system of instantaneous production, or with a fixed lag, it is appropriate to take account of the capital-output ratio. When, however, output is received in a different time sequence, the investment problem becomes one of comparing the cost of a given input with the present value of its future output.

There may also arise a question whether to use a simple or a compound interest formula in comparing the present value of two investments with different time profiles of income.

Fourth, in a desegregated model—one that examines individual projects in various sectors of the economy—the task of associating specific outputs with appropriate inputs becomes still more difficult as a result of complementarities and external economies. Manufacturing and distribution may have measured ICORs as low as 2, while electricity and railways may be as high as 16.

But manufacturing has the low ratio only under marginalist conditions; or if it is assumed that markets have already been linked by transport, that materials can be cheaply assembled, and that energy is available, as needed, at constant cost.

To the extent that each sector uses intermediate products and services from other sectors and that big (supra-marginal) projects are the most crucial ones for the development process, a focus on sectoral capital- output ratios as guides to investment decision has limited value.

One obvious objection which can be made to the method of calculating the aggregate capital requirements of the LDCs on the basis of a stable overall capital-output ratio is that this implies the assumption of constant returns to scale for the expansion of the economy as a whole.

This assumption is justified by the mature phase of the advanced countries to which the Harrod- Domar growth model is intended to apply. In LDCs, agriculture predominates in national production and is subject to diminishing returns.

In Myint’s language:

“We cannot apply the assumption of a stable overall capital-output ratio to the underdeveloped countries unless we can show at the same time how to counteract the general tendency towards diminishing returns.”

In the language of the growth models, the assumption of a stable overall capital-output ratio for the LDCs requires not only that a continual stream of innovations is taking place, but that they are of a land-saving character, enabling a progressive substitution of capital and labour for natural resources.

In spite of this objection, the concept of an overall capital-output ratio has enjoyed considerable popularity.

It is often defended on the ground that it offers a useful basis for testing:

(1) The consistency of the desired target rate of growth in national income, and

(2) The available resources of a developing country.

But, in reality, we cannot get very far in testing the economic development plans of a country unless we are prepared to go behind the overall ratio into the structural factors which determine it. The national income or output is not a homogeneous thing but is made up of different goods and services, each having widely varying capital-output ratios.

The sectoral capital-output ratios are very high for some items, notably transport and communications and public utilities. Next in order of high capital-output ratios come housing and capital-goods industries. Manufactured consumers’ goods industries—together with other distributive and service industries—generally have lower capital-output ratios.

The capital-output ratio in the agricultural sector of the underdeveloped countries is generally likely to be low, although some of the big irrigation and river valley projects require vast sums of capital Characteristically, the expansion of agricultural output in these countries depends not only on capital inputs such as fertilisers and improved equipment, but also on improvements in technical knowledge, marketing, credit, or land tenure, for example, which are not directly reflected in the capital-output ratio.

Now the overall capital-output ratio is nothing but the average of these different sectoral capital-output ratios weighted according to the quantities of the different goods and services which are to be produced. Thus, before we can calculate the overall ratio we must specify the proportions of the different constituent items which are to make up a proposed rate of increase in the national output.

But this barely scratches the surface of the problem of testing the consistency of an integrated economic development plan. For one thing, the target figures of increase in outputs of various items are not given independently of each other. Many of them are required not only for final consumption but also as intermediate goods or inputs in the production of other items.

In testing, therefore, the consistency of the target figures of items and the resources available for them, we must take into account not only the direct requirements but also the indirect requirements of capital. Furthermore, these complex input-output relationships should be tested not only for a given year, but continuously over the whole period of the Plan.

This means that, for each of the intervening years, say, during a Five-Year Plan, the rates of expansion of the different sectors must be phased so that they dovetail into each other, without any sector lagging behind their concerned time-table and holding up the others.

For, if this happens, shortages and excess capacities will develop and this will alter the effective capital- output ratios in the sectors which have gone out of alignment with the general plan. By the time we have gone through the consistency of an integrated development plan in this way, it does not help us much further to ‘sum up the whole thing’ in the form of an overall capital-output ratio.

Yet a great deal of importance has been attached to this ratio. Perhaps the proximate reason is that it offers a convenient shorthand basis for making out the case for increasing economic aid to the LDCs.

Despite these objections—assuming other things equal—when they are not, inability to decide between the gross and net measurements and the difficulty of imputing outputs to inputs, either in time or by sectors, the ICOR is widely calculated and used as device for projecting the overall investment requirements associated with plans for the expansion of outputs from estimates of investment.

Says Kindleberger “Its predictability as suggested is weak. In the short run, it is markedly variable. But over longer periods of time, averaging the annual marginal rate appears to produce meaningful overall results. This is in large part, no doubt, the result of the law of large numbers in which opposing movements cancel out. The ICOR has, in fact, been remarkably similar in a large number of countries, averaging somewhere near 3.3: 1.”

Other Investment Criteria:

The major objective of economic planning is to bring about rapid development of an economy. Development means sustained growth in per capita output. This obviously, calls for a high rate of capital formation or investment. This, in turn, necessitates an appropriate investment policy.

This will enable us to take into account considerations that are of importance in investment policy as also considerations on the basis of which investment rules or criteria have been advocated by various writers. But each may not always lead to the correct answer in every situation. In economic theory, capital and labour are assumed to be separately allocated in single units to different uses.

In national planning, however, it is more convenient to consider the decision to install a given productive process or plant, representing the allocation of a group of inputs in specified quantities, as the basic choice. Investment criteria are customarily formulated for “projects” of this sort, since they form the basis for the decisions of planning authorities. This procedure recognises that very small productive units are uneconomical, and it permits a consideration of different scales of output.

We discuss below a number of investment allocation suggestions or rules that have found their way into the literature of economic planning and development from time to time. It has to be noted at the outset that the development of an adequate theory is only the first step in formulating economic policy.

A related point may also be noted in this connection. The choice of techniques can be considered as a choice among projects producing the same output from different input combinations.

In this way the allocation procedure can be divided into two steps:

i. The choice of the best technique for a given type of product, and

ii. The decision whether to produce the commodity at all.

1. MP Criterion:

The ICOR criterion was rejected later on simply because it assumed a capital theory of value, i. e., that no other inputs were needed or that they were free of cost. If this condition is not fulfilled, it becomes necessary to switch to the marginal product of capital which takes into account the relative contribution of other factors. If this is calculated by discounting the stream of future benefits and the stream of future costs of other factors C_p it becomes (V_p – C_p)/K.

Only under certain conditions can this marginal productivity of capital serve as the criterion for investment under which all projects should be undertaken in order of their values, as long as is greater than the market rate of interest or the cost of borrowing money.

In the absence of any market imperfection this is the private marginal productivity of capital. To quote Kindleberger- “There are two underlying assumptions—the existence of competition and the absence of external economies or diseconomies. The former ensures that the return to a factor equals its marginal product, and the latter ensures that the private marginal product is equivalent to social marginal product”. This point will be taken up again soon.

2. SMP Criterion:

If there exist discrepancies between actual price-and competitive price—external economies or diseconomies or distortions—then private marginal product must be modified into a third criterion, social marginal product (SMP), or

 

 

where E_p is the present value of the stream of distortions, plus or minus, between private and social profitability. One can, of course, bundle up taxes and subsidies and distortions from social value in V_p and C_p, reserving pure external economies and diseconomies for E_p. If this is done, benefits and costs are to be calculated at a “shadow price”, rather than a market price, i.e., a price which departs from the market price so as to reflect the true social benefit or cost.

To quote Kindleberger again:

“The shadow price of benefits may be higher or lower than the market price, depending on the direction of the distortion. Equally, the divergence may be in either direction for costs. An overvalued exchange rate may underestimate the cost of imported equipment or materials. And in the presence of large numbers of unemployed, the going rate may overstate the social cost of labour. At the limit, if the shadow price of labour is zero and no other distortion or externality exists, substituting social marginal product for private marginal product may have the effect of returning us to the capital output ratio.”

SMP emphasises aggregate output, or, rather, the maximisation of the output that is attributable to the current investment effort. But it is the stream of future investments that is significant for long-term development. SMP fails to take account of what happens to the final product during any period.

Rather, what happens to the final product determines, in part, the investment rate in the future. Secondly, SMP ignores changes in the nature and quality of the factors of production that may, in part, be an indirect consequence of the current investment allocation.

To quote Leibenstein: SMP criterion does not allow for the following important elements:

(1) The indirect effect of the investment allocation on the expansion of the growth factors, that is, on the expansion of entrepreneurship, on the increase in the quality of the labour force, and on the expansion of skills;

(2) The effect of the investment allocation on future saving habits and, therefore, on the future rate of investment;

(3) The effect of the investment allocation and policy on the future consumption just for population maintenance or on the expansion of the growth agents;

(4) The indirect effect of the investment allocation on the rate of population growth, which, in turn, is a consideration in determining what happens to per capita output.

3. Growth Criterion:

Galenson and Leibenstein have suggested a fourth criterion, according to which that project should be chosen which maximises growth, not in the short run, but over a longer period of time. To quote an expert view- “In a disaggregated growth model, different projects not only have different outputs immediately because of differences in productivity. They may also have different impacts on future investment because the productivity of each is associated with a different marginal propensity to save.”

To illustrate, if one project is labour-intensive and results in large wage payments, whereas another has a high proportion of income accruing to rent or to interest and dividends, the amount reinvested in the future from the income produced is likely to be higher from the second than from the first. Its “marginal per capita reinvestment quotient” (MPCRQ) is higher.

If the marginal propensity to save is assumed to be positive, but if no savings occur until after a certain level of income has been reached (as is true of poor nations), the investment criterion becomes

 

 

where C_w is wage costs. So, to maximise growth, one should equalize in every use not the marginal productivity of capital (nor the SMP) but the MPCRQ. In particular, “one should favour capital-intensive over labour-intensive projects on the ground that the former produce more savings than the latter.”

The Galenson-Leibenstein criterion has been criticised on two main grounds. They favour skewed income distributions as an outcome of investment decision mainly due to their concern with the impact of higher employment and wages on population growth. But income skewness may not be enough if the marginal propensity to save differs between factor shares.

As Ricardo pointed out long ago, reinvestment came from profits, while rent was entirely spent on consumption. In a three-factor model, one should emphasise the high return in the form of to profits, not the low return to labour, since, historically, low wages combined with high rents have led to growth to the same extent, for example, as high wages, high profits and low rent.

The criterion has also been criticised for its readiness to sacrifice present for future consumption, at heavy social cost for today’s population. It appears that the SMP criterion and the MPCRQ criterion are related in a way which depends on the rate of interest. When the rate of interest is low and is nearly zero, future output is valued nearly as much as today’s.

Social marginal product will then be maximised by choosing highly capital-intensive projects which accelerate growth. Thus the SMP criterion converges to the MPCRQ. Says Kindlegerger- “With high rates of interest, on the other hand, growth in the future is much less valued than growth in the short run, and the Galenson-Leibenstein gloss on the Chenery criterion has little, if any, significance.”

4. Cost-Benefit Analysis:

Capital is not the only scarce resource, even in an LDC. Yet the exclusive use of the ICOR a means of selecting which projects to fund implies that capital alone is scarce. Other resources are scarce as well. Each good has an opportunity cost. In truth, all goods (or services) with positive prices are scarce in a market system.

The point is that their scarcity can be measured by their alternatives foregone- using labour to build a bridge means that an irrigation ditch remains unbuilt; using land to grow paddy means that it cannot be used to grow wheat; and so on.

So a more adequate and effective investment criterion should allow for the scarcity of all factors of production in leading to decisions about which activities should be emphasised in the developmental process.

The resource-allocation technique by which all factor inputs can be properly evaluated is known as cost-benefit analysis (henceforth CBA). Quite recently this allocative technique is being extensively used by governments and public sector authorities all over the world. CBA provides the potential for systematic investment decision making. It does not however guarantee that feasible investment projects will be made in reality.

The moot point is that “as a means for systematic evaluation of the benefits and the costs associated with alternative investment projects and for the comparison of otherwise seemingly unrelated projects and their net productivity to society, benefit-cost analysis represents a tool of incomparable value.”

Here we just spell out the bare elements in the benefit-cost analytical process. Consider a simple situation where we know the present value of the future stream of benefits (V) for a project, the present value of the costs of factors other than capital (Q) and the capital necessary for the project (K).

For small projects the marginal productivity of capital is Using the marginal productivity of capital (rather than the capital-output ratio) an investment criterion at least allows quantitatively for the scarcity of the complementary factors of production.

One further variant of CBA takes into account the future savings and capital formation that occur as the result of the inclusion of a particular project in an overall development plan. Different projects have different effects—not only on the generation of total output and income but on the distribution of that income as well. There are various recipients of income generated by a project having differing marginal propensities to save.

The conclusion that emerges is that, other things being equal, those projects should be chosen which are supposed to distribute their benefits more heavily in favour of capital-owners. The shortcomings of such a policy recommendation may now be explored.

“Redistribution of income through project choice emphasising greater capital intensity and higher savings has so many possibilities for diversion of resources that our skepticism of its wisdom has purely economic justification. If we add the political considerations implied in a regressive redistribution of income, it seems a deficient investment criterion at best.”

Since the information needed for overall economic analysis is available to a very limited extent in LDCs, there has been a considerable effort to derive decision rules or “investment criteria” that can be based on partial analysis.

H. B. Chenery groups the various suggestions into three categories:

(1) Factor-intensity criteria;

(2) Marginal productivity criteria;

(3) Programming criteria based on accounting or shadow prices. We have already discussed criterion (2).

Here we may furnish further details in this regard.

Although these various approaches often lead to contradictory results, each has some merit as a form of decision rule, if properly qualified. In general, the theoretically more valid formulations require more information and must be replaced by cruder approximations when adequate data are not available.

Since a major part of development economics has been devoted to the discussion of investment criteria, it is perhaps important and rather instructive to identify the sources of conflict among them and to specify the circumstances under which each may be approximately correct.

A. Factor-Intensity Criteria:

The simplest approach to any allocation problem is to concentrate on the scarcest resource. Since this is often capital in LDCs, it seems reasonable to choose the technique that uses the minimum amount of capital to produce a given output.

The same logic is applied to the choice of factors of production- an LDC is advised to produce and export commodities that use relatively less capital per unit of output and to import items requiring more capital. Buchanan was among the first to state this criterion for investment in LDCs to base policy recommendations upon it.

The “minimum capital-output ratio” criterion is valid only under the following three restrictive conditions:

(1) Either capital is the only scarce factor in the system, or other inputs are so abundant relative to capital that the latter is the dominant element in determining cost differences.

(2) Either the same output is produced by each investment alternative, or the market values used to compare the different products coincide with their social values.

(3) Production takes place under constant costs.

A closely related allocation criterion is the capital intensity- the ratio of capital to labour. If the same production functions exist in all countries and if capital is scarce relative to labour in the LDCs, then comparative advantage in the latter can be identified by low capital-labour ratios.

It may be noted that this approach does not assume that labour has zero opportunity cost, as does use of the capital-output ratio, but only that the ratio of labour cost to capital cost is lower than in the country’s trading partners.

A principal criticism of the use of both these ratios is that they ignore the existence of other factors of production, such as natural resources. If either labour or natural resources has a significant opportunity cost, the capital-output measure must be replaced by the more general marginal productivity of capital criterion.

B. Marginal Productivity Criteria:

A more comprehensive allocation criterion is the social marginal product of a given unit of resources in a given use. Where the factor-intensity criteria are at best correlated only with the increase in national income produced by a project, the productivity criteria try to measure the increase.

There are several forms of marginal productivity criterion. But they are all alike in assuming that the government controls, directly or indirectly, a certain fraction of the investible resources of the country and wishes to allocate them in such a way as to maximise future welfare.

Since the productivity criteria are usually applied to investment projects rather than to single units of capital, they are “marginal” only in the sense that a project normally constitutes a small fraction of the total capital invested in a given year. For very large projects a breakdown into smaller units would be more appropriate.

The Static SMP Criterion:

As proposed by Kahn the social marginal product (SMP) is a general equilibrium concept which is conventionally defined as the net contribution of a marginal unit (project) to the national product. The related decision rule is to rank investment projects by their SMP and to go down the list until the funds to be allocated are exhausted.

Alternatively, any project having an SMP above a given level can be approved. Kahn’s arguments against the simple capital-intensity criteria appear to have been generally accepted although he admits that a lower capital-output ratio may be a useful guide when other information is lacking.

The Marginal Reinvestment Criterion:

A sharp criticism of the SMP criterion was made by Galenson and Leibenstein who challenge some of its basic premises. They would substitute a different social welfare function in which the aim is to maximise per capita income at some time in the distant future rather than to maximise a discounted stream of income over time.

They also assume severe restrictions on the policy instruments available to the government, and, in particular, deny its ability to affect the rate of saving by fiscal measures. Under these assumptions, it is necessary to take account of the division of income resulting from a project between profits and wages, since savings from the former are higher.

To maximise the total output at some distant future time, Galenson and Leibenstein easily show that the most “productive” project is not necessarily the one which maximises national income in the near future but the one which leads to the highest savings.

Since they assume that no voluntary saving or taxes can be extracted from wages, the most productive project will be the one with highest profit rate per unit of capital invested. The Assumption that profits are saved and reinvested leads to the “marginal reinvestment quotient” as decision rule to be applied in place of the SMP.

The Marginal Growth Contribution:

Eckstein has successfully reconciled the conflict between the Kahn-Chenery SMP approach and the Galenson-Leibenstein reinvestment approach, and, in so doing, he has provided a considerable generalisation of each. First, he assumes that the social objective is to maximise the present value of the future consumption stream.

With a zero discount rate, this objective approximates the long-term income objective of Galenson and Leibenstein, while with a high discount of future consumption it leads to the maximisation of income in the short term. Second, Eckstein assumes that there is a different savings (reinvestment) coefficient associated with each project, but he allows for any savings rate out of wages and profits.

From these assumptions, he derives a measure of the “marginal growth contribution” of a given project that consists of two parts:

(1) An efficiency term, consisting of the present value of the consumption stream; and

(2) A growth term, consisting of the additional consumption to be achieved by reinvesting savings.

The relative importance of the two terms depends largely on the rate of discount that is applied to future consumption. Even with a low rate of discount, the significance of the second term depends on how much variation there is in the fraction of income saved among different projects. If the savings ratio is not related to the form of income generated, then, as Bator shows, there is no conflict between maximising income in the short run and in the long-run.

C. Programming Criteria and Accounting Prices:

Both the factor-intensity ratios and the partial productivity measures assume that there is one principal restriction on the system—the scarcity of capital. They, however, ignore the fact that in allocating capital according to any one of these rules some other restriction on the system- such as the supply of foreign exchange, of skilled labour, or of a particular commodity—may be exceeded.

The programming approach to resource allocation begins with the problem of balancing supply and demand for different commodities and factors of production. Until quite recently, practical programming methods have been more concerned with ensuring the consistency of a given allocation of resources with certain targets than with testing the efficiency with which resources are used. Historically speaking, the programming approach is thus the operational counterpart of the theory of balanced growth, from which much of its conceptual framework is derived.

A link between the test of consistency (feasibility) in resource allocation and the test of productivity (efficiency) is provided by a consideration of the price implications of a given allocation. Assume that a set of production level has been worked out so as to be consistent with the available supplies of labour, capital, and natural resources, given the structure of consumer demand and the country’s trading possibilities.

These sectoral production and trade levels constitute a “feasible programme”. Any such programme implies a unique set of commodity and factor prices if the economy is in equilibrium. If production activities are assumed to operate at constant costs, linear programming provides a method of calculating the “shadow prices” corresponding to the equilibrium conditions, in which the price of each commodity is equal to its cost of production.

Prices are determined by the solution to the following set of simultaneous equations, one for each production activity included in the programme:

a,_1jP₁+ a_2jP₂ + …+ a_njP_n = 0 (j= 1 … n)

where a_ij is the input or output of commodity or factor i by activity j, and P_i is the shadow price of commodity or factor i. The input coefficients may be measured at existing prices or in other convenient units. The use of shadow or “accounting” prices in evaluating investment projects has been suggested by Tinbergen, Frisch and Chenery.

Although Tinbergen does not use a linear programming framework, his accounting prices for factors have the same meaning as shadow prices the opportunity cost implied by a given resource allocation. He suggests computing the costs associated with a project by using accounting prices; any project that shows a positive net return over cost (including capital cost) should be approved.