The Law of Equi-Marginal Utility (With Explanation)

The below mentioned article provides a close view on the law of equi-marginal utility.

Explanation of the Law:

In order to maximise satisfaction with a limited amount of money a consumer has to compare the satisfaction obtained from each rupee that he spends on different commo­dities.

If he finds that a rupee spent on one commodity gives him more utility than the same rupee spent on another commodity, he shall continue to spend money on the former till the utilities derived from the last rupee spent on the two commodities are equal.

In other words, he substitutes some units of a commodity giving more utility for some units giving less utility. As a result of this substitution that the marginal utility of the former will fall and that of the latter will rise. This will continue until the two marginal utilities are equalised. This is equal to the Law of Subs­titution or the Law of Equi-marginal Utility.

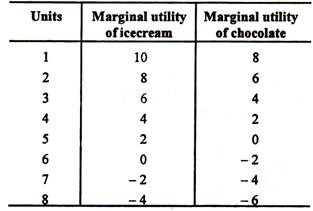
Table 4.3: Marginal Utility of Two Commodities

Suppose chocolates and ice-creams are two purchasable goods. Suppose further that the consumer has Rs. 70 to spend. Let us spend Rs. 30 on ice-creams and Rs. 40 on chocolates. What is the result? The utility of the 3rd unit of ice-creams is 6 and that of the 4th unit of chocolates is 2. As the marginal utility of ice-cream is higher the consumer would buy more of ice-creams and less of chocolates.

Suppose he substitutes one ice-cream for one chocolate so that he buys four ice-creams and three chocolates. Now the marginal utility of both ice-creams and chocolates is the same, i.e., 4. This combination of ice-cream and chocolate yields maximum total utility of satisfaction.

The total utility of 4 ice-creams would be 10 + 8 + 6 + 4 = 28 and of three chocolates 8 + 6 + 4=18 which gives us a total utility of 46. The satisfaction given by 4 ice-creams and 3 chocolates at Rs. 10 each is greater than could be obtained by any other combination of the two goods. For no other combination does this utility amount to 46.

So the conclusion is that we obtain maxi­mum satisfaction when we equalise marginal utilities by substituting the more useful for the less useful commodity. This law may now be illustrated with the help of a diagram (see Fig. 4.6).

Diagrammatic Representation:

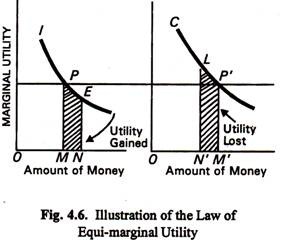
In Fig. 4.6 on the horizontal axis we measure money and on vertical axis marginal utilities. Suppose a person has Rs. 70 to spend on ice-creams and chocolates whose dimini­shing marginal utilities are shown by the two curves I and C respectively.

The consumer will gain maximum satisfaction if he spends OM amount of money (Rs. 30) on chocolates and OM’ amount of money (Rs. 40) on ice-­creams because when he buys (his combination) the marginal utilities of the two are equal (PM=PM’). Any other combination of the two goods will give less total satisfaction.

Let one representative consumer spend MN money (Rs. 10) more on ice-creams and the same amount of money, NM’ (= MN) less on chocolates. Utility lost is shown by the shaded area LN’M’ P’ and utility gain by the PMNE area. As MN = N’M’ and PM=P’M’, the LN’ MP’ (loss of utility from reduced consumption of oranges) is bigger than PMNE (gain of utility from increased consumption of apples). Hence the total utility of this new combination is less.

So the conclusion is that no other combination of ice-cream and chocolate gives as utility satis­faction to the consumer as when PM = PM’, i.e., where the marginal utilities of ice-cream and chocolate purchased are equal, with the fixed budget of the consumers i.e., Rs. 70.

The Rule of Allocation of Fixed Income:

How will a consumer distribute a given amount of money over different items of expenditure? In order to derive maximum satisfaction with a fixed budget, he will so arrange his purchases that the marginal utilities of the goods purchased are in proportion to their prices.

Thus a consumer will be in equilibrium, i.e., he will be deriving maximum satis­faction, when

MU of Ice-cream/Price of Ice-cream = MU of Chocolate/Price of Chocolate … (3.1)

This is also called the Law of Proportionality. This law can be extended to cover any number of commodities.

In case the price of one commodity rises, less of this commodity and more of others will be purchased so as to maintain the proportion. However, the above law will hold only if the consumer’s tastes and other factors remain unchanged and the commodities are perfectly divisible.

The Law of Equi-Marginal Utility and the Law of Demand:

From the Law of equi-marginal utility we can suggest an explanation of why the demand curve for a commodity is negatively sloped. In a simple situation where the consumer purchases only two commodities, say, ice-­cream and chocolate equation (3.1) above may be expressed as

MU of Ice-cream/Price of Ice-cream = MU of Chocolate/Price of Chocolate …… (3.2)

This condition can be restated as follows:

MU of Ice-cream/Price of Chocolate = MU of Ice-cream/Price of Chocolate …. (3.3)

This condition implies that the consumer wants to get the same MU per rupee spent on ice-cream and chocolate. Thus if the price of ice-cream is double the price of chocolate, he must get twice the MU from the last unit of ice-cream as from the last unit of chocolate.

We may now consider the demand curve for one of these two commodities, say ice-cream, and see why the demand curve for ice-cream slopes downward from left to right. Now, holding all other things (viz., the price and consumption of commodity; chocolate) cons­tant, we may permit the price of ice-cream to fall.

The initial equilibrium will be disturbed. But the consumer will again reach the equili­brium position by consuming more ice-cream until its MZ7 falls in the same proportion as its price has fallen. If, for instance, the price of ice-cream falls by 15% the consumer increases his purchase of ice-cream until its MU falls by exactly 15%. When this happens the ratio in (3.3) will be re-established.

This shows why the demand curve for ice-cream (or any other commodity) has a negative slope. It may be noted that the consumer adjusts his purchases of ice-cream until its MU changes in proportion to the change in its price. There is, however, no need to change the consumption of ice-cream in that proportion. If MU of ice-cream falls very fast, a little more of it will be bought; if the MU of ice-cream falls slowly, then many more units will be purchased.

In most text books it is stated that the MU of ice-cream is equated with the price of ice-cream. This statement holds only if a special con­dition is satisfied the MU and price of C are set equal to unity. The statement that holds in general is that for fixed prices and quantities of all other commodities, the quantity demanded of any commodity will always be associated with its price.

Application of the Law:

A rational consumer consciously acts on this law while allocating his limited expenditure in the purchase of differently priced goods. This means that, his expenditure is to be distributed that the same price measures equal utilities at the margin of different purchases. Every person must try to spend his limited money in such a way as to get the maximum satisfaction. This is possible if he spends his money in such a manner as to obtain equal satisfaction from the marginal units of money spent on the different commodities he purchases.

Criticisms of the Utility Approach:

The analysis so far has centered on the concepts of TU and MU. However, the concepts cannot be properly quantified or measured.

Three main defects of the utility approach are:

1. Marshallian Analysis is Inadequate:

The ‘utility’ derived by a person from a commo­dity does not depend only on the quantity of it possessed or consumed by him. It also depends upon the quantity owned and possessed by others. According to James Duesenberry the consumption habits of a person are influenced by the consumption habits of other people belonging to the community.

Thus, the demand for goods depends upon the relative standard of living. It also depends upon past incomes, when income increases people cannot adjust their habits and on spending behaviour immediately. For these reasons it can be said that the Marshallian analysis of demand is inadequate.

2. The Cardinal Concept of Utility is not Quite Acceptable:

Modern writers do not accept the cardinal means of utility. ‘Utility’ cannot be measured in precise quantitative terms.

3. The Marginal Utility of Money is not Constant:

It is improper to assume that the marginal utility of money is constant. In reality as income increases the marginal utility of money falls. This means that rupee to a rich man is less valuable than the same rupee to a poor man. However, if the relax the assumption i.e., constant marginal utility of money, the law of equi-marginal utility does not hold.

A more satisfactory method of examining an individual consumer’s behaviour has been developed by Pareto and Edge-worth, known as the ‘indifferent curve approach’.

Limitations of Law of Equi-Marginal Utility:

1. Too Much Rationality:

The law of equi­-marginal utility assumes too much rationality about the behavior of the consumer. In real life, consumers do not always make their purchases considering minutely the relative marginal utilities of the different commodities they make their purchases very often out of fancy or emotion or social needs without judging carefully their marginal utilities. In such cases the law may not operate.

2. Ignorance:

If the consumer is ignorant or blindly follows custom or fashion, he may use his money carelessly or in the purchase of wrong of wrap commodity (which way may appear to be useless to him). Dut to ignorance he may not know which consumables gives more utility and which one less. Not knowing latest custom and fashion he may not be able to make a rational use of money. Hence, his satisfaction may not be the maximum because the marginal utilities from his expense cannot be equalised.

3. Indivisible Units:

The law does not operate in the cases of the goods which cannot be divided into small parts or are not available in small units (e.g., motor cars, refrigerators, TV sets, etc.). Since in such cases the perfect adjustment of marginal utilities is not possible the law does not apply.

4. Mistake in Calculation:

The law may fail to operate if the consumer commits mistakes in calculating marginal utilities of the commodities consumed.

5. Unlimited Resources:

The law does not apply where the resources are unlimited, as is true of the free gifts of nature. In such cases there is no need of diverting expenditure from one commodity to another.

6. Utility Versus Satisfaction:

The law of equi-marginal utility states that the equa­lisation of marginal utility in all the cases of purchases maximises total utility and thus the total satisfaction of a consumer. However, ‘utility’ and ‘satisfaction’ are not the same thing; so the maximisation of utility may not lead to the maximisation of satisfaction. ‘Utility’ and ‘Satisfaction’ may not be identical, but they are closely related, that an increase of utility would cause an increase in satisfaction, cannot be denied.

7. Role of Custom and Fashion:

Moreover, due to of custom, or fashion the consumer may not be able to derive maximum satis­faction out of his expenditure, because he cannot give up the consumption of certain commodities. This is true of such things like dress or ornaments.

8. Difficulty in Measuring Utility:

The law assumes that utility can be measured. But critics have pointed out that utility, being a subjective thing, cannot be objectively measured.

9. Frequent Changes in Prices:

Due to frequent changes in prices of different goods the law may not apply. In such cases a consumer cannot make rational calculations.

Conclusion:

Despite all these limitations or exceptions the law has great practical relevance. As most of the consumers are assumed to be rational, they behave, consciously or un­consciously, in accordance with this principle for maximising the gains and minimising the losses. In short “we are not, of course, compelled to distribute our incomes according to the law of substitution or equi-marginal expenditure; but as a matter of fact we do in a certain rough fashion because we are reasonable.”

So by a process of logical analysis we can reach the conclusion that, if a person’s money income and tastes remain the same, and if the prices of all other commodities and the value of money remain unchanged, then the lower the price of the commodity the more he (or she) will buy in a given period. This con­clusion is not based on common sense. It is built on observations of human attitudes and behavior.

Because MU falls as additional units of a commodity are consumed, price must fall to make the purchase of additional units worthwhile. The fall in price also makes it worthwhile to substitute more of the commodity in question for units of other commodities whose prices have not changed.