Producer’s Equilibrium: MR-MC Approach, Perfect Competition and Diagrams

Producer’s Equilibrium: MR-MC Approach, Perfect Competition and Diagrams!

Conditions of Producer’s Equilibrium – MR-MC Approach:

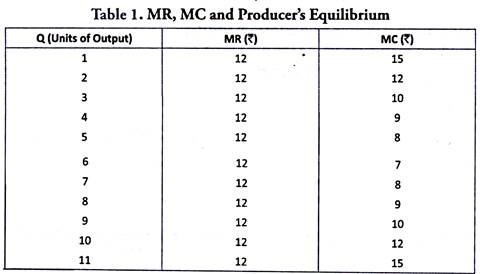
Producer’s equilibrium is often explained in terms of marginal revenue (MR) and marginal cost (MC) of production. Profit is maximized (or a producer strikes his equilibrium) when two conditions are satisfied – (i) MR = MC, and (ii) MC is rising (or MC is greater than MR beyond the point of equilibrium output). Let us understand the significance/rationale of these conditions with reference to Table 1.

In Table 1, MR = MC in two situations – (i) when 2 units of output are produced, and (ii) when 10 units of output are produced. However, while in situation 1 (when output = 2 units) MC is falling, in situation 2 (when output = 10 units) MC is rising. A producer will strike his equilibrium only when MC is rising.

Implying that the equilibrium will be struck when 10 units of output are produced, not when 2 units of output are produced. Reason is simple. Given the price, falling MC only increases the difference between TR and TVC (recall, ΣMC = TVC, and ΣMR = TR). So that TR – TVC tends to rise, or that profits tend to rise in a situation of falling MC.

Accordingly, it would be an irrational decision for a producer to strike his equilibrium in a situation of falling MC. It is only when MC is rising that a producer would strike his equilibrium. Thus, equilibrium will be struck when MR = MC = 12, and MC is rising. The producer will maximize profits when 10 units of output are produced. Let us illustrate this point further with reference to Table 1.

Table 1 offers us two different situations when MR = MC, as under:

We find that the difference between TR and TVC tends to rise, as output is increased from 2 to 10. In fact, it is only when output = 10 units that the profit (π) is maximum. If output is increased beyond 10 units, π will reduce.

Thus, if 11 units of output are produced, ΣMR = 132, while ΣMC = 115, so that π = TR – TVC =132 – 115 = 17 (which is less than 20 when output = 10).

It is only when MR = MC, and when MC is rising that a producer will reach the point of equilibrium, where profit is maximized.

Diagrammatic Illustration:

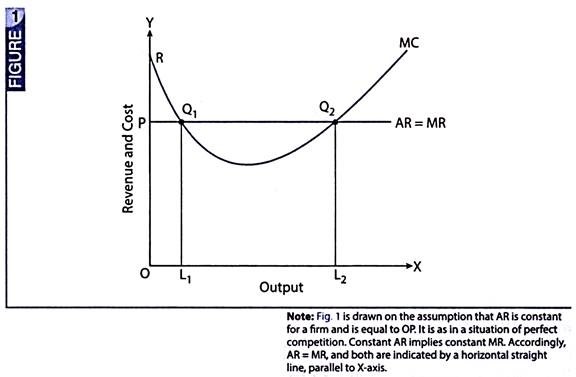
Fig. 1 illustrates producer’s equilibrium in terms of MR and MC approach:

In Fig. 1, AR is assumed to be constant as under perfect competition. Constant AR implies constant MR. Thus, both AR and MR are indicated by a horizontal straight line parallel to X-axis. MC curve is shown to be U-shaped, as usual. MR is equal to MC in two situations – (i) at point Q₁ when output = OL₁, and (ii) at point Q₂ when output = OL₂. In situation 1, MC is falling but in situation 2, MC is rising. Equilibrium of the producer will be struck at point Q₂ when – (i) MR = MC, and (ii) MC is rising.

It is at point Q₂ that the profit (= TR-TVC) is maximized, not at point Q₁. In fact, Q₂ is a situation of profit while Q₁ is a situation of loss. This is how we can prove it.

It is situation of loss to the firm. In such a situation, it would not be wise for the producer to undertaker production of the commodity.

Corresponding to situation 2, when MC is rising, at point Q₂, we find that:

TR = OL₂Q₂P, and

TVC = OL₂Q₂R

Evidently, TR > TVC

This indicates the existence of profit. Accordingly, the producer will strike his equilibrium only in situation 2 when (i) MR = MC, and (ii) MC is rising.

With reference to Fig. 1, producer’s equilibrium is struck at point Q₂ when output = OL₂. It is here only that the two conditions of equilibrium are satisfied – (i) MR = MC, and (ii) MC is rising.

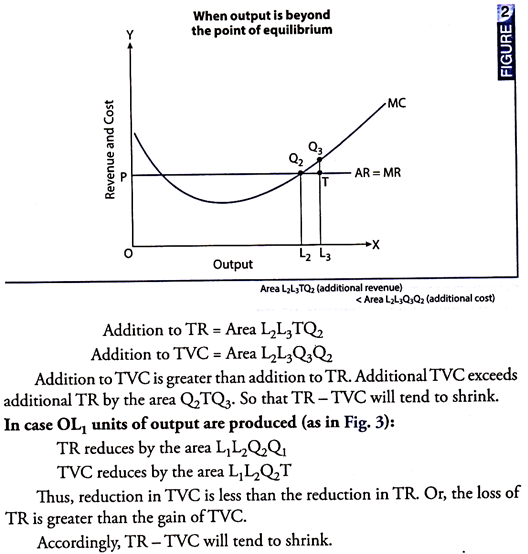
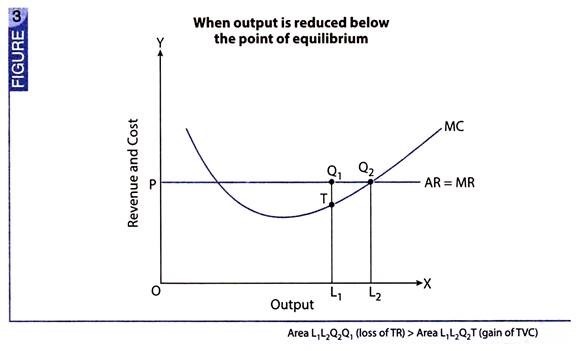
What happens when a unit more or a unit less is produced than OL₂ units of output?

Answer is that in both the situations π will be less compared to the situation when OL₂ units of output are produced. Figs. 2 and 3 illustrate this situation.

In case OL₃ units of output are produced (as in Fig. 2):

Thus, any departure from the state of equilibrium (when MR = MC, and MC is rising) would only mean that the difference between TR and TVC will tend to shrink, or that the profits will not be maximised.

Do All Firms always Maximise their Profit?

‘No’ is the answer. Profit maximisation is only a goal. A firm may or may not achieve it. After all there are firms which close down, owing to losses. However, a notable point in this context is that a firm may suffer losses, and yet continue to stay in the market; it does not suspend its production activity. Yes, this happens in the short period.

Because in the short period, a firm is confronted with 2 sets of costs – (i) fixed cost, and (ii) variable cost. Fixed cost is incurred even when output is zero. A firm has to bear the loss of fixed cost even when production is stopped. Accordingly, a firm may decide to continue production so long as variable costs are covered. Thus, production may continue as long as TR ≥ TVC, even when a producer is in losses (as he is not covering his fixed costs).

Of course, in the long period, when all costs are variable costs, a firm will undertake production only when all costs are covered. Otherwise, it will quit the industry.

Firm’s Equilibrium when price (AR) is not constant:

When price is not constant, a firm can generally sell more of a commodity by lowering its price. Implying that AR curve slopes downward. In such a situation, MR curve also slopes downward and at a rate faster than AR.

Even, in such situations, equilibrium of a firm is struck when two conditions are satisfied:

(i) MR = MC, and (ii) MC is rising.

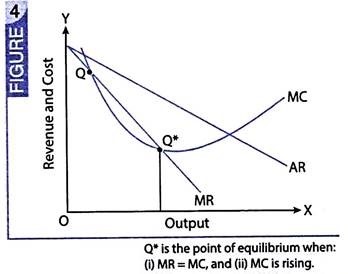
This is illustrated through Fig. 4:

Both at points Q and Q* MR = MC. But at point Q, MC is falling. It is only at point Q* that (i) MR = MC, and (ii) MC is rising.

Accordingly, a firm will strike its equilibrium only at point Q*.