The below mentioned article provides short notes on price determination under discriminating monopoly.
The main reason for a monopolist to use price discrimination is to obtain an increase in his total revenue and his profits.
By selling the quantity determined by the equation of his MC and MR at different prices the monopolist realizes a higher total revenue and hence higher profits as compared with the revenues he would receive by charging an uniform price. We will begin from the simple case of a monopolist who sells his product at two different prices.
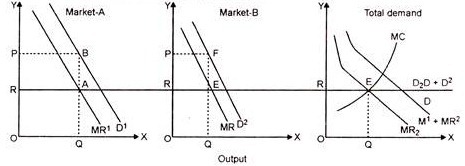
It has been assumed that the monopolist sells his product in two segregated markets— Market A and Market B, each of them having a demand curve with different elasticity. The demand is more elastic in Market B than Market A.
The demand curve of Market A is D’ whereas Market B has demand curve as D” MR ‘ and MR ” are the marginal revenue curves of Market A and Market B respectively. The total demand curve D is found by the horizontal summation of D’ and D “. The aggregate marginal revenue (MR) is the horizontal summation of the marginal revenue curves MR’ and MR “. The Marginal Cost curve is depicted by the curve MC.
The priced terminating monopolist has to decide:
(a) The total output that he must produce.
(b) How much to sell in each market and at what price, so as to maximise his profits.
ADVERTISEMENTS:
The problems have been discussed as under:
The total output of the product, to be produced may be defined by the point of intersection of the MC and the aggregate MR curve of the monopolist. In the above figure both MR and MC curves intersect at point E. Thus, OQ output is produced. In each market he must equate the marginal revenue with the marginal cost. In Market A OQ1 output and in Market B OQ “output is sold. Thus total profits is maximised when the monopolist equate:
MC = MR1 = MR2
In Market A the total revenue are OPBQ1 and OPFQ2 in Market B. Total revenue OPBQ1 and OPFQ2 is more than the total revenue obtained in case of the simple Monopoly.