Basic Concepts of Macroeconomics

Basic Concepts of Macroeconomics!

Economic Models:

Models are theories that summarise the relationship among economic variables. Models are useful because they help us to dispense with irrelevant details and to focus on important economic relations more clearly.

A model is a description of reality with some simplification. To simplify analysis each model makes some assumptions which must be explicitly stated when a model is formulated.

A model may be expressed in terms of equations or diagrams. Of course, a model can also be expressed verbally.

However, diagrams and equations are the most convenient method of expressing relationship among economic variables.

Models have two kinds of variables: exogenous and endogenous variables Exogenous Variables come from outside the model — they are inputs into the model. Endogenous variables come from inside the model — they are the output of the model. In other words, exogenous variables are fixed at the moment they enter the model, whereas endogenous variables are determined within the model. The purpose of a model is to show how the exogenous variables affect the endogenous variables.

For example, let us see how we can develop a model for bread. We assume that the quantity of bread demanded, Q^d, depends on the price of bread, P_b and on aggregate income Y. This relationship is expressed in the equation Q^d = D (P_b, Y) where D denotes the demand function.

Similarly, we assume that the quantity of bread supplied, Q^s, depends on the price of bread, P_b, and on the price of flour, P_f, since flour is used to make bread. The relationship is expressed as Q^s = S (P_b, P_f), whereas S denotes the supply function. Finally, we assume that the price of bread adjusts to equilibrate demand and supply: Q^d = Q^s. These three equations compose a model of the market for bread. Economic relationships involved in a model may be of different types.

Firstly, the relations could be behavioural. For example, consider the saving function S = S(Y), which states that saving (S) is a function of income (Y).

Secondly, relationship between the variables could be technical. The technical relationships follow from technological considerations. For example, consider the production function Y = F (K, L) which states that total output (Y) produced is a function of total capital employed (K) and total labour employed (L). This relationship is determined by the technological consideration underlying the production process. Hence it is a technical relationship.

Thirdly, the relationship may be definitional. Such relationships follow from the very definitions of the variables. For example, if Y_m represent money income, Y_r represents real income and P represents price level, then Y_m = Y_r X P represents a definitional equation.

A model must be complete. Mathematically, this means that number of equations should be equal to the number of Variables. For example, in our demand and supply model for bread, we have three unknowns and three equations. Hence the model is determinate. In the Simple Keynesian Model of income determination we have three equations: (i) C = C(Y) (Consumption function); (ii) I = I (Investment function); (iii) Y = C + I (Equilibrium condition) we have three equations. Hence the model is determinate. We need to distinguish between variables and parameters in a model.

The parameters are constants in relation to the variables in a model. For example, in a simple linear consumption function: C = a + bY, C and Y are variables while a and b are parameters. When any of the parameters changes the consumption function shifts its position.

Flexible versus Sticky Prices:

One crucial assumption of macroeconomic models arc the adjustment of wages and prices. Economists normally presume that the price of a good adjusts to equilibrate demand and supply, they assume that, at the going price, suppliers have sold all they want and demanders have bought all they want.

This assumption is called market clearing. For answering most questions, economists use market-clearing models. But the assumption of continuous market clearing is not entirely realistic. For markets to clear continuously, prices must adjust instantly to changes in demand and supply. However, many wages and prices adjust sluggishly.

Many labour contracts often set wages for longer years. Many firms leave their product prices unchanged for long periods of time. Although market clearing models assume that all prices and wages are flexible, in real world, we know, prices and wages are not so flexible.

The apparent stickiness of prices does not make market-clearing models useless. They might not describe the economy at every instant, but they do describe the equilibrium toward which the economy slowly moves. Thus most macroeconomists believe that market-clearing models are a good approximation to reality, especially in dealing with long-period issues. Prices and wages are flexible in the long-run.

However, for studying short-run issues, the assumption of price flexibility is less useful. Over short periods, many prices arc fixed. Thus, many economists believe that price stickiness is a better assumption for studying short-run issues.

Monetarist and Keynesian:

The Keynesian View:

Keynesian macroeconomists are those who advocate detailed intervention to ‘fine tune’ the economy in the neighbourhood of full employment and low inflation. They seek to control inflation by direct controls of wages and prices and to reduce unemployment by stimulating aggregate demand, using monetary and fiscal policy.

They would use discretion to stimulate the economy in a depression or to hold the economy in a boom. They are not in favour of announcing policy change beforehand, so as to deter speculation. They modify their policy in the light of current and best-available forecasts. The intellectual leaders of this group are F. Modigliani, J. Tobin and many others in British universities.

The Monetarist View:

Monetarists prefer the government to have policies towards a limited number of macroeconomic variables such as money supply, government ex­penditure, taxes, etc. They advocate the adoption of fixed rules for the behaviours of these variables. For example, a widely advocated rule is that the money supply should grow at a certain fixed percentage rate per year.

Another rule widely advocated by them is that the government budget should be balanced over a period of four to five years. In any event, all policy interventions which do occur should be announced as far ahead as possible so as to enable people to take account of them in planning their own economic affairs.

The intellectual leader of this school is M. Friedman, R. Lucas and many others in the American universities.

We should not form the impression that the Keynesian/Monetarists division is one that follows neat political boundaries. Although there is some tendency for there to be an association between monetarism and Conservatism, and between Keynesianism and liberalism/socialism, that association is far from perfect. Monetarists range all the way from diehard libertarians to orthodox Marxists. Keynesians do not go quite so far to the right, but they do go a long way in that direction.

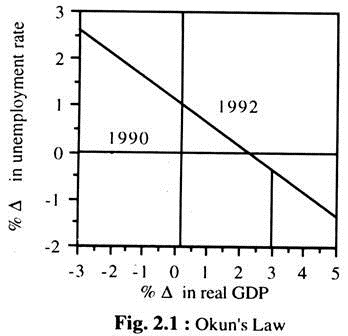
Okun’s Law:

A relationship between real growth and changes in unemployment rate is known as Okun’s law. Okun’s law says that the unemployment rate declines when the growth is above the trend rate of 2.25 per cent. Specifically, for every percentage point of growth is real GDP above the trend rate that is sustained for a year, the unemployment rate declines by one-half percentage point.

This relationship is stated in equation; ∆u = – 0.5 (y – 2.25) where ∆u denotes the change in the unemployment rate, y is the growth rate of output. The use of the formula can be seen as: Suppose growth rate in a given year is 4.25 per cent. That would imply a reduction of unemployment rate of 1.0 percent [= 0.5 (4.25 – 2.25)].

Fig. 2.1 shows the change (∆u) in unemployment rate on the vertical axis and the % ∆ in real GDP on the horizontal axis. Each point represents one year.

Ex-post and Ex-ante:

An economic concept can he defined either in ex-post or ex-ante sense. Ex-ante magnitudes refer to as planned or intended or desired magnitudes. They are determined by the decisions taken by different economic units. For example, in any year, different economic units plan to save some amount. The sum total of such planned savings is the total ex-ante saving of the economy.

Ex-post concepts refer to actual magnitudes. Thus, ex-post national income refers to the actual national income of a country. Similarly, ex-post saving refers to the actual saving. Ex-post magnitudes can be measured only after they have occurred. There is, however, no guarantee that the ex-ante value of a variable will be necessarily equal to ex-post value.

Thus, ex-ante saving may not be equal to ex-post saving, people may not be able to save what they plan or desire to save. If individuals succeed in realising their saving plans, i.e. when each individual saves an amount which is equal to plan saving, their ex-ante total saving will be equal to ex-post total saving.

Similarly, ex- ante total investment will be equal to ex-post total investment if all the investment plans are realised. Ex-ante values arc relevant for determining equilibrium values of different variables. For example, the equality of ex-ante savings and ex-ante investments determines the equilibrium level of income in the Keynesian model of income determination. Similarly, equilibrium price is determined by the equality of ex-ante demand and ex-ante supply and so on.

Equality and Identity:

An equation represents a relationship between several variables which is true for some specific values of the variables but not true for all values. For example, let us consider the relation y = 2x + 5. It is not true for all possible values of x and y. But it is true for certain values of x and y only. An equation is characterised by “=” sign while an identity is denoted by “≡” sign.

We can solve an equation and can determine the value of the variables for which the equation is satisfied. An equation represents a functional relationship. For example, suppose it is assumed that aggregate consumption depends on the level of Y of the economy. Then assume that the consumption is a linear function of income (Y). This equation can be written as C = a + bY where a and b are parameters.

It represents an equation and not an identity. It can be tested. But an identity cannot be tested. It is always true by definition. Hypothesis about economic behaviours can be represented by an equation. But identities cannot represent a behavioural relationship.

However, an identity is a relation between several variables which is true for all possible values. For example, when it is said that (x – y)² ≡ x² – 2xy + y² it is true for all possible values of x and y. Hence it is an identity. An identity is denoted by “≡” notation. An identity is always true by definition. An identity cannot be solved for determining the values of the variables since it is satisfied for all values of the variables. An example of an identity can be given from macroeconomics. Income be either consumed or saved.

Hence total income will always be equal to the sum of total consumption and total saving. It is true for all levels of income. Thus, it is an identity. We can write identity as Y ≡ C + S where Y is total income, C is total consumption and S is total savings. We cannot use this identity to determine the equilibrium level of income. An accounting relationship such as the equality between actual saving and actual investment represents an identity. An identity is a mere tautology and it explains nothing.

Static and Dynamic Analysis:

When the variables involved refer to the same point in time (or period of time), then this analysis is known as static analysis. On the other hand, if the variables involved refer to different points of time (or periods of time) then this analysis is called dynamic analysis.

When we say that the quantity demanded during a period of time depends on price in that period of time, then this represents a static relationship. For example, if savings of the economy during a period of time depends on the level of income of that period, then this represents a static relationship.

On the other hand, if it is said that planned supply in any period depends on the price of the previous period, i.e. x_t = F(P_t-1) where x_t is planned supply in period t and P_t-1 is the price in the previous period, then this represents a dynamic relationship.

Suppose, we are considering a Simple Keynesian Model of income determination, in which there are three equations: consumption is a function of income, C = C(Y), then the investment function I = I̅₀ and the equilibrium condition where Expenditure equals income: Y = C + I. Solving these three equations give us equilibrium values of all these variables. This analysis is a static analysis; all the variables refer to the same period of time.

Further, the time element is not considered in the determination of equilibrium values of the variables. Similarly, the determination of equilibrium price by the equality of supply and demand is another example of static analysis.

Static analysis is concerned with the determination of equilibrium. However, it does not concern itself with the time it takes to reach an equilibrium or with the path to follow to reach the equilibrium. This is the concern of dynamic analysis.

The useful static analysis is known as comparative statics. In comparative static analysis one equilibrium position is compared with another equilibrium position. In static analysis there are several parameters which are assumed to be constant at a particular level. If any of these changes the equilibrium position will also change.

When we compare one equilibrium position with another corresponding to different values of the same parameter, we call it comparative static analysis. The Keynesian multiplier analysis is an example of comparative static analysis.

In the comparative static analysis one equilibrium position is compared with another equilibrium position without analysing the process of movement. Such a process of analysis is unnecessary if the speed of adjustment is very quick. However, when the speed of adjustment is slow, we need dynamic- analysis to get a complete picture of the movement from one equilibrium to another.

Dynamic analysis is necessary for the following reasons. First, dynamic analysis is necessary to consider the stability of the system. An equilibrium is known as stable if any disturbance from the equilibrium brings the system back to equilibrium again. For example, if we start from a disequilibrium position and then want to know whether the system moves towards equilibrium or not we require to analyse the time path of the relevant variable. This is known as dynamic analysis.

Second, since adjustment of one variable takes time to cause a change in another variable, there are lags in many functions. The presence of these lags requires dynamic analysis. Third, there are certain variables which depend on the rate of growth of other variables. Such problems require dynamic analysis.

Stocks and Flows:

Stock and flow variables are an important distinction in macroeconomics. A How variable has a time dimension. It is always measured over a period of time. A stock variable has no time dimension. It is measured at a given point in time. The stock variable is just a number, not a rate flow of so much per period. For example, the concepts like total money supply, total bank deposits, etc. are stock concepts whereas the concepts like national income, national output, total consumptions, etc. are flow concepts.

When we measure the national income we consider a period of time, namely one year. Thus national income is measured as a flow per year. Similarly, total investment, total saving, total consumption etc. are expressed as amount per year — so they are flow concepts. But the total supply of money is a stock concept which is measured on a particular point in time. Thus, flow variable must specify the period of time to which this flow refers.

If we talk about the income of an individual we must mention the time period of this income flow. If we say that the individual has an income of £ 10,000, it is meaningless because we have not mentioned the time period. If the time period is one month, it means something — that the individual is earning £ 10,000 per month or £ 1,20,000 per year. Thus, the time period of a flow variable is very important.

However, the stock variable is measured without any reference to time period. In economics we use both flow variables and stock variables and it takes a little practice to master these concepts. The main test is whether a time dimension is needed to give the variable meaning.

The distinction between stock and flow variables can be explained with the help of an example. The bathtub is a classic example used to illustrate stocks and flows. The amount of water in the tub is a stock: it is the quantity of water in the tub at a given point in time.

The amount of water coming out of the tap is a flow: it is the quantity of water added to the tub per unit of time. But the units with which we measure stocks and flows differ. We say that the bathtub contains 100 gallons of water, but that water is coming out of the tub through the tap at a rate of 5 gallons per minute.

Stocks and flows are often related. In the bathtub example, these relations are clear. The stock of water in the tub represents accumulated water, and the flow of water represents the change in the stock. When developing theories to explain economic variables, it is often useful to think about whether the variables arc stocks or flows and the relationships between them.

Here are more examples of stocks and flows that we study in macro­economics:

1) A consumer’s wealth is a stock; his income and expenditure are flows.

2) The amount of capital i n an economy is a stock; the amount of investment is a flow. For example, if K₀ is the stock of capital at the beginning of a year and if K₁ is the stock of capital at the end of the year then (K₁ – K₀) = I₀ is the flow of investment during the year.

3) The number of unemployed people in a given year is a stock; the number gaining their employment is a flow.

4) The government debt is a stock; the budget deficit is a flow. The ratio of two flow magnitudes having the same time dimension is a pure number without any time dimension. For example, APC = c/y is the ratio of consumption flow to income How and is also a pure number without any time dimension. Again, the derivative of a flow with respect to another flow is also a pure number without any time dimension. Thus, the marginal propensity to save, MPS = ∆S/∆Y has no time dimension ant is a pure number.

Concept of Equilibrium:

Equilibrium is a concept borrowed from mechanics where we get the idea of equilibrium system of forces. In mechanics a system of forces is said to be in equilibrium if two forces making to move the body in opposite directions are counter-balanced. Thus, an equilibrium situation is a state of rest.

In economics we use the term to mean that a single price for a product is established in a market and when no economic forces are being set up to change that price. In other words, in equilibrium, the price and quantity of a commodity match both consumers’ and producers’ expectations and thus there is no discrepancy between the actual and desired prices and quantities.

Consequently, market is cleared and there are no involuntary holdings of unsold stocks. The equilibrium behaviours of consumers and producers — whether in a single market or in the economy as a whole — is characterised by the fact that there exists no feeling of urgency on the part of the buyers and sellers to change their behaviour.

In contrast, disequilibrium situation is one in which some buyers and sellers feel compelled to change their behaviour because forces are at work that change their circumstances. By changing their behaviour, however, they change the circumstances of other producers and consumers who may initially have been in equilibrium. A disequilibrium sets in motion a chain of adjustment and readjustment processes; for example, on the stock market, buyers and sellers change their behaviour daily in response to changing circumstances.

The economy as a whole would be in equilibrium when the planned demand for output is equal to planned supply of output. The whole economy would be in equilibrium when aggregate demand equals aggregate supply.

Equilibrium analyses are of two types: partial equilibrium and general equilibrium. In partial equilibrium analysis equilibrium is reached in one market assuming that all other things remain unchanged. However, in general equi­librium analysis, different markets of the economy are interdependent. In microeconomics, partial equilibrium analysis is generally used. But, in macroeconomics, general equilibrium analysis is usually used as in the classical or the Keynesian macroeconomic systems.

An equilibrium is a state of rest in which no economic forces are being generated to change the situation. In a market for a good, such a state of rest can be said to exist when there is neither excess demand for nor excess supply of the good.

An equilibrium is said to be a stable equilibrium when economic forces lend to push the market towards it, or any divergence from the equilibrium position generates forces which tend to restore the equilibrium. However, the equilibrium could be unstable when a small change in equilibrium price sends the system further and further away from equilibrium.

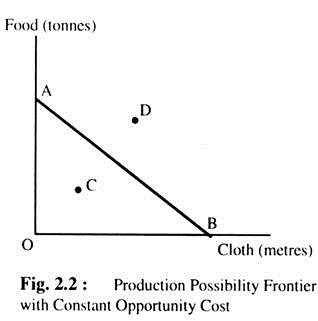
Production Possibility Frontier with Constant Opportunity Cost:

A production possibility frontier joins together the different combinations of goods and services which a country can produce using all available resources and the most efficient techniques of production. Let us assume that a country produces only two goods: food and cloth. Fig. 2.2 shows the different combinations of these commodities which may be produced.

The horizontal axis measures the quantity of cloth in metres and the vertical axis measures the quantity of food in tonnes. The line AB is the production possibility frontier which shows that when all resources are efficiently employed in the production of food, OA tonnes can be produced and when all resources are employed in the production of cloth. OB metre can be produced.

All points over the production possibility frontier represents combination of cloth and food which can be produced when all resources arc efficiently employed. All points inside the line, such as C. represent combinations which can be produced using less than the available resources or by using them less efficiently. Points outside the line, such as D, represent combinations which are unattainable.

The slope of the production possibility frontier (OA/OB) measures the opportunity cost in terms of food of producing extra 1 metre of cloth. Similarly, the slope (OB/OA), measures the opportunity cost in terms of cloth of producing extra 1 tonne of food. This means that every additional metre of cloth produced requires OA/OB tonnes of food be forgone and vice versa.

The slope of the production possibility curve is also known as the marginal rate of transformation. When the production possibility frontier is drawn as a straight line, the opportunity cost and the marginal rate of transformation remain unchanged no matter how much cloth is produced. This is called constant opportunity costs which is unrealistic. It means that all factors of production can be used equally efficiently in either the production of food or the production of cloth.

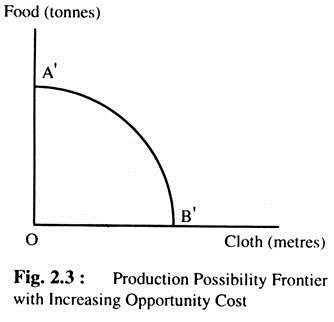
It is more realistic to assume that some factors are more efficient in the production of cloth and others arc more efficient in the production of food. Thus, as more and more metres of cloth are produced, it becomes necessary to move into cloth production resources which are more efficient in the production of food. This is a case of increasing opportunity costs. The case of increasing opportunity cost is represented in Fig. 2.3.

Cross-section and Time Series Data:

Economic data can be classified into cross-section and time series data. Cross-section data refer to the statistics collected from different groups of population during the same period. For example, suppose data collected on consumption expenditure of a group of families during a given year. This is a cross-section data. Similarly, if incomes of different groups are collected during a year, this will give us cross-section data. Cross-section data are useful in order to verify different functional relationships which are supposed to be invariant over time.

On the other hand, time series data is recorded with reference to time periods. The businessman is perhaps more interested in using time series data as an aid to business forecasting, particularly in areas of sales, so that in an appropriate time budget allocations may be made for investment and advertising for the year ahead. When we collect national income figures of a country for different years it represents time series data.

If we are to plot a time series data in a graph we plot time (t) on the horizontal axis and the value of the variable on the vertical axis. Time series data are necessary when we are interested in the analysis of seasonal or cyclical variations.

Cross-section data are more useful in order to verify functional relationships which are supposed to be invariant over time. Both types of data are useful in the study of macro­economics. For example, consumption function hypothesis may be tested either with reference to cross-section or time-series data.

Aggregate Demand and Supply:

The key concepts in macroeconomics are aggregate demand and aggregate supply. Here we provide a brief preview of these concepts and their interaction. The level of output and the price level are determined by the interaction of aggregate demand and aggregate supply. Under some conditions, employment depends only on total spending or aggregate demand. At other time, supply limitations are an important part of the policy problem and have to receive important attention.

From 1930s to the 1960s macroeconomics was very much demand determined. But in recent years the emphasis has been shifted, and aggregate supply and supply side economics have gained in importance. This shift of emphasis and interest are fostered by the slow growth and high inflation experienced in the 1970s.

What are the relationships between aggregate demand and supply, output and employment, and prices? Aggregate demand is the relationship between spending on commodities and the level of prices. When unemployment is high, increased spending — or an increase in aggregate demand — will raise output and employment with little effect on prices. For example, during the Great Depression of the 1930s, it would certainly be appropriate to use expansionary aggregate demand policies.

But if the economy is close to full employment, increased aggregate demand will be inflationary. The aggregate supply side of the economy has to be introduced. The aggregate supply curve specifies the relationship between the amount of output firms produce and the price level.

The supply side not only tells us how successful demand expansions will be in raising output and employment, but it also has a role of its own. Supply shocks can reduce output and raise prices, as was the case in the 1970s when the price of oil increased sharply. Conversely, policies that increase productivity — and hence aggregate supply — can help reduce inflationary pressure.

The Unemployment Rate:

One aspect of economic performance is how well an economy uses its resources. Since an economy’s workers are its chief resource, keeping workers employed is a concern of policy-makers. The unemployment rate is the statistic that measures the percentage of those people who want to work but could not find any job.

Unfortunately, unemployment has been a recurring feature of Western capitalist economy and its eradication has become one of the major policy objectives.

The labour force is defined as the sum of the employed and unemployed, and the unemployment rate is defined as the percentage of the labour force unemployed.

Labour Force = Number of Employed + Number of Unemployed.

Unemployment Rate = Number of Workers Unemployed x 100/ Total Labour Force

A related statistic is the labour-force participation rate, the percentage of the adult population in the labour force:

Labour-Force Participation Rate = Labour Force x 100/Adult Population

Natural Unemployment:

Natural unemployment is defined as that which exists even when the overall demand for labour is equal to its supply at the prevailing level of real wages. Or, it is that unemployment which exists when the labour market is in equilibrium. Such unemployment persists because of frictions in the economy which prevent some workers from taking up the available jobs. Natural unemployment may be illustrated in Fig. 2.4 where DD_L is the demand curve for labour and SS_L is the supply curve of labour.

The curve EE shows the actual number employed at different wage rates and, because of frictions in the economy, actual employment always falls short of the demand for and supply of labour. At the real wage rate OW₁, the demand and supply of labour are just equal at OL but actual employment is only OA, thus At is the ‘natural’ unemployment.