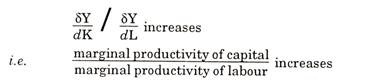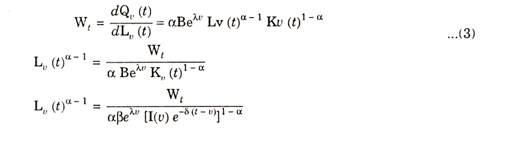Models of Technical Change in Economic Growth (With Diagram)

The below mentioned article provides an overview on the models of technical change in economic growth.

Subject-Matter:

Technical progress plays an imperative role in influencing the pace of economic growth. It is the technical change which results in an increased output per unit labour. It signifies a comprehensive phenomenon and, therefore, denote different things in different contexts.

Technical change refers to change in the production function embodying all techniques.

Thus, technical change in the context of economic development must result in more output for the same resources or the same amount of output. It could occur following a change in any of the production variables. Thus, it may result due to a change in kinds of physical capital, in the quality of labour or even in the organisation of these resources.

Harrod-Dommar model is based on the assumption of fixed coefficients of production and gives rise to the knife edge problem. Kendrick, Kaldor and Solow and others have been the most consistent critics of this approach who have tried to demonstrate the role of technological changes in the growth of an economy.

In this way, the nature of the technical progress is most important determinant of the individual factor productivities. It brings a proportionate increase in the productivities of all the factors. Therefore, the model of technical change is based on the controversy over neutral and non-neutral technical change.

Neutral and Non-Neutral Technical Changes:

A technical change is said to be neutral if it is neither capital saving nor labour saving i.e. it is neutral in its effect in the sense that neither of the two factors become more or less important at the margin. There are two definitions of neutrality. One is given by Prof. Hicks and the other by Prof. Harrod.

A. Hicks views on Neutrality. According to Prof. Hicks, neutrality is “An invention which raises the marginal productivity of labour and capital in same proportion”. Thus, a technical change is neutral if the ratio of marginal product of capital to that of labour remains unchanged at constant capital labour ratio.

A technical change is termed as labour saving if it raises the marginal product of capital relative to that of labour at a constant capital labour ratio.

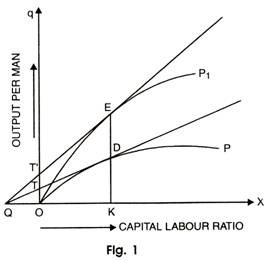
Hick’s neutral technical change is explained in the figure 1 by comparing points on two different; production functions:

The output per man q is represented along with vertical axis and capital labour ratio is represented along with horizontal axis. OQ measures the marginal product of labour and capital. OP is the production function before technical change and OP₁ is the production function after technical change. Taking, production function OP, the slope of tangent QTD measures the marginal product of capital and OT measures the marginal product of labour.

Since slope QT shows the marginal product of capital, say u, we can express it as:

u = OT/ OT or OQ = OT/u

Hence OQ measures the ratio between marginal product of labour OT and marginal product of capital ‘u’, Hicks neutral technical progress requires that if technical change shifts the production function upwards from OP to OP₁, the ratios of two marginal products must be same on vertical line from X-axis like KE where it passes through the production functions at points D and E, respectively.

Hicks Neutral Technical Progress:

The condition is that the tangent QE on the higher production function OP, must originate from the point Q to left of O, like the tangent before the technical change. In the figure, the tangent QE on the production function OP₁originates from Q.

When both the tangents QE and QD on production functions OP and OP₁originate from Q, only then the ratios between marginal product of labour and capital will be equal i.e. the ratio between the marginal product of labour and capital after the technical progress (OW₁/u₁) must be equal to the ratio between the marginal products of labour and capital before technical progress (OW/u)Therefore, the ratio between the marginal product of labour and capital is equal at points D and E on the vertical line KE.

This situation can be expressed as under:

Q = Q (t) f (K, L)

where Q — Total output

K — Inputs of capital

L — Inputs of labour

A (t) — Index of technical progress. It measures accumulated effects of shift overtime and is an increasing function of t.

On the basis of the definition of Hicks neutrality, we can define labour saving and capital saving technical changes, which Mrs. Joan Robinson’s terms biased technical progress.

Capital—Saving Technical Change:

A technical change is capital saving if it raises the marginal product of labour relatively to capital, at constant capital labour ratio. The given output will require less capital relative to labour.

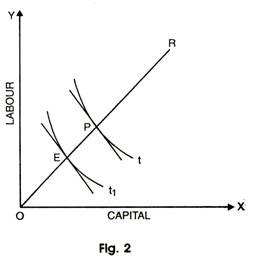
This is illustrated with the help of a diagram 2 given below:

This shows that a shift in production function resulting from the capital saving technique would be one where, for a given K

This type of technical change is capital saving, i.e. it would be possible to produce a given level of output with less capital relative to labour than before the introduction of technique.

If the amount of capital used is reduced absolutely and that of labour rises, the technical change is absolutely capital saving and labour using. On the other hand, if the technique leads to a fall in the amounts of both the inputs, but the fall in the input of labour is less compared to that of capital, the technique is said to be relatively capital saving.

Labour-Saving Technical Change:

A technical change is labour saving if it raises the marginal product of capital relative to labour at constant capital labour ratio. The given output would require less labour relatively to capital i.e. for a given K

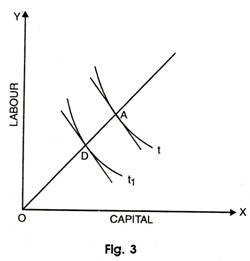
and it would be possible when the technical progress causes a rise in the productivity of capital proportionately more than that y of labour i.e. it is possible to produce a given level of output with less labour relative to capital. The figure 3 given below shows the case of labour saving technique.

Where t is the isoquant before the technical progress and t₁ after the technical progress. If the amount of labour used is reduced absolutely and that of capital rises than the technical change will be absolutely labour saving and capital using. On the other side, if the technique leads to a fall in both factors but the fall in amount of labour is proportionately more than that of capital, the technique is said to be relatively labour saving.

The precise manner in which relative and absolute amounts of labour and capital used will change as a result of technical change will depend upon the factor elasticities of substitution and product elasticities of demand.

Therefore, it will depend upon the elasticities of substitution between capital and labour in the economy, for these will help to determine what effects the technical change has on the prices of the two factors. It will also depend upon the elasticities of demand for the product of various industries that make up the economy.

In Hicks Neutral Technical progress, the factor shares remain constant if factor proportions and relative remunerators of labour and capital are constant. If he consider figure 1, it implies that between D and E if the slope of the production function OP₁ at E is greater than the slope of production function OP at D in the same proportion as the output KE is greater than KD, then the technical progress is Hicks Neutral.

This means that when the amount of capital is changed, the marginal product of capital increases in the same proportion as total output. In other words, between D and E, the proportion of total output which is paid out of profits and wages remains constant. Again, it is also as when the elasticity of substitution between labour and capital is equal to unity.

Criticism:

Hicks neutrality has been criticized on many grounds.

Firstly, it is a rigid type of definition even when large factors of production are involved. Secondly, the dependence of Hicks Neutrality on demand elasticity and substitution elasticities makes it a cumbersome tool of analysis. It is quite unrelated to the intrinsic character of the innovation itself such as the elasticity of demand for product and factor.

Lastly, the Hicksian neutrality is built within the frame work of static economic analysis.

Harrod’s View on Neutrality:

Prof. Harrod in his book “Towards a Dynamic Economics” has defined neutral technical progress in a different way. His definition is based on capital output ratio. According to him, neutral technical progress is one which leaves capital output ratio unchanged, provided that rate of profit remains constant. Thus, Harrod’s neutrality of technical progress requires the constancy of both the rate of profit r and capital output ratio K/Y.

If the rate of profit remains unchanged and the capital output ratio increases, the technical progress would be labour-saving. On the other hand, if after the technical progress, the capital output ratio falls, while the rate of profit remains constant, the technical progress would be capital saving.

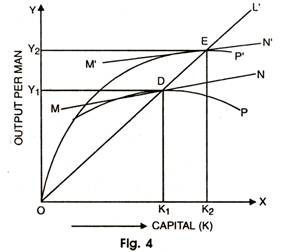
Harrod Neutrality is explained with the help of a diagram 4.

In this diagram, the capital per man (k) is measured along X-axis and output per man (q) is along Y-axis. OP is the production function before the technical change and OP is after technical change. The capital output ratio at D on production function OP is OK₁/OY₁ and at point E on production function OP’ is OK₂/OY₂.

Since the ray OL passes through both points D and E, the capital output ratios are equal i.e. OK₁/OY₁= OK₂/OY₂. Harrod’s neutrality also requires that the rate of profit must remain constant along with a constant capital output ratio after technical progress.

This implies that the marginal productivity of capital must be same at both points of D and E on production functions OP and OP’, respectively which, in turn, requires that the slope of the production function OP at point D must be equal to the slope of the production function OP’ at point E. In other words, the tangents at D and E must be parallel to each other.

In figure 4, the tangent MN at D is parallel to the tangent M’N’ at point E i.e. the marginal products of capital at D and E are the same, Thus, Harrod neutral technical change as shown by shifting the production function OP upwards to OP’ depicts the equality of the capital output ratio at D and E as represented by the ray OL passing through them.

Thus, the equality of slopes at D and E shows that the rate of profit is constant.

Harrod’s definition of neutral technical progress is superior to that of Hicks because it is applicable to a dynamic situation rather than a static situation. It forms a most significant part of the theory of economic growth because it uses the concept of capital output ratio which is indispensable in modern growth analysis.

In Harrod neutral technical change, there is no direct reference to labour as it is entirely based on the relationship between capital and output but capital labour ratio and output labour ratio may change without technical change, Therefore, in Harrod’s neutrality, the rise in output per machine would be in the same proportion as the rise in the output per man.

Harrod’s neutrality implies that the distribution of income between profits and wages does not change because under perfect competition, the factors are paid according to their marginal product. As it leaver the marginal product of capital unchanged, the factor shares as between capital and labour, must also remain unaltered.

The assumption of constant capital output ratio implies that the capital stock and labour force must grow at same rate. It follows that the incomes of the capitalists would grow at same speed at which the wages of the workers rise. If a technical progress is capital saving in Harrod’s sense, this will raise the share of labour in the national output and reduce that of capitalists at a constant rate of interest.

On the other hand, a labour saving technique will reduce the share of labour in national output and increase that of capitalists with constant rate of interest.

Harrod’s neutrality can be shown in the form of production function as:

Q = [F K, A (t) L]

Here Q is a function of F and K and A (t) L means that the given constant return to scale on equal proportionate rise in capital (K) and in effective labour units [A (t) L] must lead to proportionate rise in national output Q. The constant rate of interest increases the efficiency of labour in whole economy.

However, “With population growth, there is an increase in the number of men at work, Harrod neutral technical progress, the GNP rises at given rate.” The difference is that with Harrod’s neutral technical progress, income per head increases, with population growth it remains the same.

As Mrs. Joan Robinson and Uzawa have shown on the strict definition, Harrod’s neutral technical progress raises income at same rate whatever may be the level of the capital output ratio. It is this which measures technical progress. Solow has shown that the Harrod’s neutrality can be purely capital augmenting technical progress with production function.

Q = F [A (t) K, L]

A (t) — Index of technical progress.

The technical progress is both Hicksian Neutral and Harrod’s Neutral.

If the elasticity of substitution between labour and capital is unity and there is no change in the distribution of income, it is Harrod’s Neutral. The neutral change is in Hick’s sense if the given labour force capital remains unchanged and distribution of income is the same. It is Harrod-neutral if with given labour force, capital increases in the same proportion as national output and distribution of income is the same.

Disembodied Technical Change:

During 1956, M. Abramovitz wrote papers followed by J.W. Kendrick and R.M. Solow to measure the contribution of technical change to economic growth. They treated technical change as disembodied.

Disembodied technical change is purely organizational which permits more output to be produced from unchanged input, without any new investment. It refers to any kind of shift in the production function that leaves balance between capital and labour undisturbed in the long run.

The production function for such technical change is written as:

Q = F (K, L; t)

Q — Output

L — Labour input

K — Capital input

t — Technical change.

Taking Hicks neutral technical change as a basis, Solow postulated the production function in special form as:

Q = A (t) F (K, L)

(A) — Index of technical change.

Thus, accordingly, “Such a production function implies that technical progress is organizational in the sense that its effect on productivity does not require any change in the quantity of inputs. Existing inputs are improved or used more effectively”.

The growth rate of output is equal to the rate of technical change plus a weighted average of growth rate of capital and growth rate of labour Assuming linear homogenous production function, these weights add to one and we have Q/Q =A/A + at (K/K) + (1- at ) L/L

Where does indicate time derivatives and ‘at’ is the capital elasticity of output.

Solow proceeded to focus on rate of technical change. He stated “By using data on the share of capital and labour and the rates of growth of capital per head and output per head, the contribution of the residual is obtained after calculating the contribution of capital.

This residual is attributed to technical progress”. He concluded that during 1940-49 the average growth rate of output per head in United States could be attributed 12.5 per cent to increase in capital per worker and the residual 87.5 per cent to technical change.

Criticism:

The above conclusions tried to undermine the rate of investment in contrast to technical change in growth process.

According to Phelps, “The results of this approach provided a wave of investment pessimism”. Whereas Rosenberg, writes, “They provide a wide response on the part of the economists wakened as it were, from their dogmatic slumber.” They become sceptical about such a large size of the residual. Abramowitz admitted, “It is a measure of out ignorance”.

Griliches puts that, “Residual approach is not of much use in understanding the growth process as it is based on the concept of a production function which is not very useful if it is not a stable production function and if there are very large unexplained shifts in it”. Critics further observed that, “Residual approach tended to ignore other influences like improvements in the quality of labour due to education”.

This approach is based on the unrealistic assumptions of perfect completion, constant returns to scale and complete homogeneity of capital stock. Denison, Kendrick, Griliches tried to quantify and break down the residual into further components.

They contended that the residual was not a catch all and that changes in output were due to changes in the quantities and qualities of inputs, in economies of scale and advances in knowledge rather than the result of technical change, assuming a stable production function.

Embodied Technical Change:

Solow modified the residual approach himself based on disembodied technical change where in capital stock is regarded as homogeneous and technical change floats down from the outside.

According to F.H. Hahn and R.C.O. Mathews, “In this model, new capital accumulation is regarded as the vehicle of technical progress. Technical progress increases the productivity of machines built in any period compared with machines built in previous period, but it does not increase productivity of machines already in existence. Technical progress is embodied in new machines. Machines alterably embody the technology of their date of construction. Machines built at different dates are therefore, qualitatively dissimilar and cannot in the general case be aggregated into single measure of capital. A separate production function is needed for each vintage. Total output is the sum of output of all the vintages in use”.

Assumptions:

This model is based on the following assumptions:

1. Capital stock consists of machines of different vintages or built at different dates.

2. New machines are more productive than old ones.

3. Technical change proceeds at some given proportional rate.

4. Machines embody all the latest knowledge at the time of construction but do not share in any subsequent improvements in technology.

5. Technical change effects only new machines.

6. Only gross investment in new machines is considered in the model and the production function is linear homogeneous.

7. Technical change proceeds at some given proportional rate.

8. The production function is linear homogeneous of the Cobb- Douglas type.

The total output Qv (t) at times t from the machines of each vintage v is given by Cobb-Douglas production function

 

 

 

 

 

 

 

 

 

 

“The picture is one of the continuum of capital goods of various vintage and corresponding productivity, subject to an exponential life table”, according to Solow. At each moment of time the labour force is reshuffled over the existing capital goods. This total output is determined by integrating over all layers of capital stock”.

Solow states that if we assume competition in the labour market, all homogeneous labour must receive the same wage regardless of the age of capital on which it operates.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solow calls J as an effective stock of capital which is productivity weighted sum of all surviving capital goods representing all early technological levels.

But the capital goods of smaller vintages receive a smaller weight than new capital goods. He further adds that average age of capital can be lowered by increasing the saving rate and thereby average quality of machines in use can be raised. Thus output per man can be raised.

Appraisal:

The model of disembodies technical change is based on the assumption that capital stock is completely homogeneous. New machines are better than old machines and technological progress is embodied in new machines. In the former, capital labour ratios change at all times along the Cobb-Douglas production function.

But in the latter, once a machine is constructed, it has labour requirements.

In other words, “Each machine is designed to be worked with given crew of men and the size of crew cannot be changed”.

Mrs. Joanson has rightly observed that this model is said to have ex-ante substitutability between labour and capital and ex-post fixed coefficients or no ex-post substitutability. Phelps puts that it is a putty day model-putty ex-dante and clay ex-post. On the other hand, the model of disembodies technical change is one of ex-ante and ex-post substitutability or a partly model.

Limitations:

The drawbacks of technical change model are listed as below:

1. It is based on the assumption of perfect competition and hence fails to consider factor market imperfections.

2. Solow assumes that machines depreciate exponentially. But Stieglitz points out that this may be reasonable assumption for telephone poles but not for machines.

3. It does not take into account the influence of wage expectations on machine construction. An investor forms expectations of wage rates extending into future before constructing a machine. In that case, the real wage rate will not equal the marginal productivity of labour on the machine of a given vintage and type, but it will equal the average output per man on the least efficient machine.

4. The entire model is based on the hypothesis that machines are of different types and new machines are better than old ones.

5. The assumption on which this model is based relate to fixed labour requirements. This is unrealistic for an economy with a higher output per man which may have lower capital labour ratio.

6. It concentrates only on technological progress embodied in new machines and ignores the problems of inducing innovations through the process of learning and investments in research.