Marginal Revenue and Price Elasticity of Demand

Marginal Revenue and Price Elasticity of Demand!

The concept of marginal revenue is closely related to price elasticity of demand. The word ‘margin’ always refers to anything extra. Therefore, marginal reve­nue is obtained by selling an extra unit of a com­modity (or service).

But a more accurate definition of marginal revenue goes as follows:

Marginal revenue is the rate of change in total rev­enue as output (sale) changes by one unit. In perfect competition, marginal revenue is al­ways equal to average revenue or price, because the firm can sell as much as it like at the going market Price.

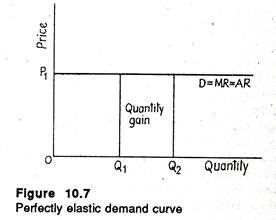
So the firm is a price-taker. This is so be­cause the demand for the firm’s product is com­pletely elastic. The following one is a perfectly elastic demand curve. This is often used to depict the price and output behaviour of a firm under pure competition. Here dP/dQ = 0.

Therefore, the graphing of P in terms of Q in Figure 10.7, has a slope of zero. In other words, the demand curve is completely (perfectly) elastic. In fact, if E_p → ∝ the expression MR = P[1-(1/E_p)] reduces to MR = P.

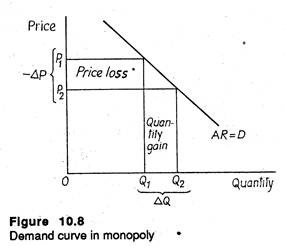
But in monopoly or imperfect competition, a firm is a price maker. Therefore, it has to reduce price to sell more. See Figure 10.8 which shows that the de­mand for the firm’s product is not completely (per­fectly) elastic.

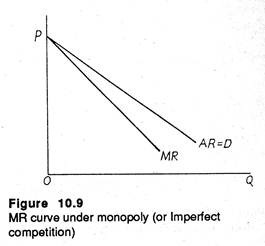
As a result marginal revenue (MR) and average revenue (AR), both fall (when price is lowered). But MR falls faster than AR and the MR curve lies below the AR curve. See Figure 10.9 now. The explanation of the difference between price and marginal revenue is simple enough: in adding the last unit to sale quantity Q, the firm accepts a reduction of price for all the pre-marginal (Q-1) units.

For all markets other than purely competi­tive ones, the MR function is lower than the de­mand (or average revenue) functions for all units produced expect the first. In other words, MR is less than price. MR may be expressed as MR = dTR/dQ, where the dTR with respect to dQ is the first deriv­ative of the total revenue function.

MR can alternatively be expressed as:

MR = P[1-(1/E_p)]

where MR = marginal revenue,

P = market price of the product, and

E_p = the price elasticity of demand for the product

The above formula is very useful when the de­mand function has a known constant price elastici­ty. Business managers must estimate the value of MR in order to arrive at decisions about price and output.