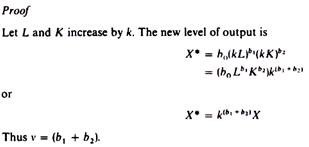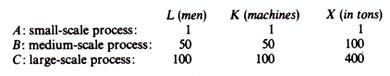Laws of Production: Laws of Returns to Scale and Variable Proportions

The laws of production describe the technically possible ways of increasing the level of production. Output may increase in various ways.

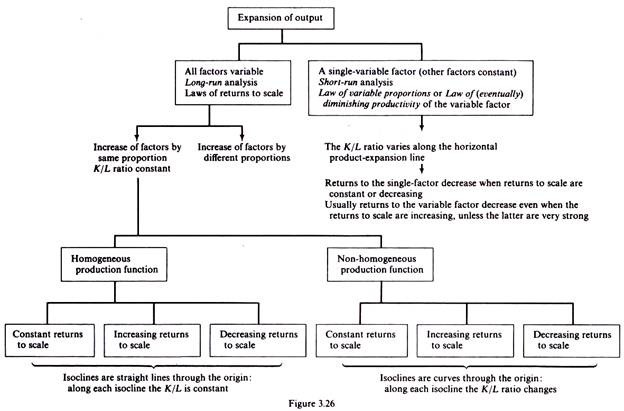
Output can be increased by changing all factors of production. Clearly this is possible only in the long run. Thus the laws of returns to scale refer to the long-run analysis of production.

In the short run output may be increased by using more of the variable factor(s), while capital (and possibly other factors as well) are kept constant.

The marginal product of the variable factors) will decline eventually as more and more quantities of this factor are combined with the other constant factors. The expansion of output with one factor (at least) constant is described by the law of (eventually) diminishing returns of the variable factor, which is often referred to as the law of variable propor­tions.

We will first examine the long-run laws of returns of scale.

A. Laws of Returns to Scale: Long-Run Analysis of Production:

In the long run expansion of output may be achieved by varying all factors. In the long run all factors are variable. The laws of returns to scale refer to the effects of scale relationships. In the long run output may be increased by changing all factors by the same proportion, or by different proportions. Traditional theory of production concentrates on the first case, that is, the study of output as all inputs change by the same proportion. The term ‘returns to scale’ refers to the changes in output as all factors change by the same pro­portion.

Suppose we start from an initial level of inputs and output

X₀ = ƒ(L, K)

and we increase all the factors by the same proportion k. We will clearly obtain a new level of output X*, higher than the original level X₀,

X = ƒ(kL, kK)

If X* increases by the same proportion k as the inputs, we say that there are constant returns to scale.

If X* increases less than proportionally with the increase in the factors, we have decreasing returns to scale.

If X* increases more than proportionally with the increase in the factors, we have increasing returns to scale.

Returns to scale and homogeneity of the production function:

Suppose we increase both factors of the function

X₀ = ƒ(L, K)

by the same proportion k, and we observe the resulting new level of output X

X* = ƒ (kL, kK)

If k can be factored out (that is, may be taken out of the brackets as a common factor), then the new level of output X* can be expressed as a function of k (to any power v) and the initial level of output

X* = K^vƒ (L, K)

or

X* = k^vX₀

and the production function is called homogeneous. If k cannot be factored out, the production function is non-homogeneous. Thus A homogeneous function is a function such that if each of the inputs is multiplied by k, then k can be completely factored out of the function. The power v of k is called the degree of homogeneity of the function and is a measure of the returns to scale

If v = 1 we have constant returns to scale. This production function is sometimes called linear homogeneous.

If v < 1 we have decreasing returns to scale.

If v > 1 we have increasing returns to scale.

Returns to scale are measured mathematically by the coefficients of the production function. For example, in a Cobb-Douglas function

X = b₀L^b1K^b2

the returns to scale are measured by the sum (b₁ + b₂) = v.

For a homogeneous production function the returns to scale may be represented graphically in an easy way. Before explaining the graphical presentation of the returns to scale it is useful to introduce the concepts of product line and isocline.

Product lines:

To analyze the expansion of output we need a third dimension, since along the two- dimensional diagram we can depict only the isoquant along which the level of output is constant. Instead of introducing a third dimension it is easier to show the change of output by shifts of the isoquant and use the concept of product lines to describe the expansion of output.

A product line shows the (physical) movement from one isoquant to another as we change both factors or a single factor. A product curve is drawn independently of the prices of factors of production. It does not imply any actual choice of expansion, which is based on the prices of factors and is shown by the expansion path. The product line describes the technically possible alternative paths of expanding output. What path will actually be chosen by the firm will depend on the prices of factors.

The product curve passes through the origin if all factors are variable. If only one factor is variable (the other being kept constant) the product line is a straight line parallel to the axis of the variable factor (figure 3.15). The K/L ratio diminishes along the product line.

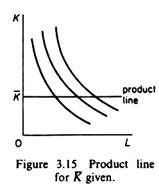
Among all possible product lines of particular interest are the so-called isoclines.An isocline is the locus of points of different isoquants at which the MRS of factors is constant. If the production function is homogeneous the isoclines are straight lines through the origin. Along any one isocline the K/L ratio is constant (as is the MRS of the factors). Of course the K/L ratio (and the MRS) is different for different isoclines (figure 3.16).

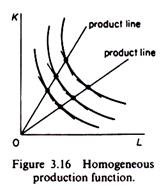
If the production function is non-homogeneous the isoclines will not be straight lines, but their shape will be twiddly. The K/L ratio changes along each isocline (as well as on different isoclines) (figure 3.17).

Graphical presentation of the returns to scale for a homogeneous production function:

The returns to scale may be shown graphically by the distance (on an isocline) between successive ‘multiple-level-of-output’ isoquants, that is, isoquants that show levels of output which are multiples of some base level of output, e.g., X, 2X, 3X, etc.

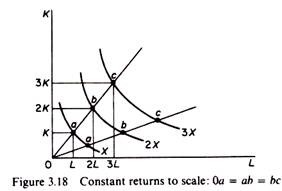
Constant returns to scale:

Along any isocline the distance between successive multiple- isoquants is constant. Doubling the factor inputs achieves double the level of the initial output; trebling inputs achieves treble output, and so on (figure 3.18).

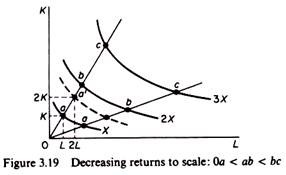
Decreasing returns to scale:

The distance between consecutive multiple-isoquants increases. By doubling the inputs, output increases by less than twice its original level. In figure 3.19 the point a’, defined by 2K and 2L, lies on an isoquant below the one showing 2X.

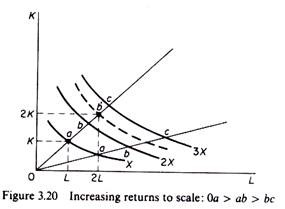
Increasing returns to scale:

The distance between consecutive multiple-isoquants decreases. By doubling the inputs, output is more than doubled. In figure 3.20 doubling K and L leads to point b’ which lies on an isoquant above the one denoting 2X.

Returns to scale are usually assumed to be the same everywhere on the production surface, that is, the same along all the expansion-product lines. All processes are assumed to show the same returns over all ranges of output either constant returns everywhere, decreasing returns everywhere, or increasing returns everywhere.

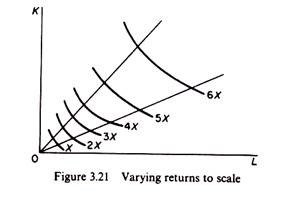
However, the techno­logical conditions of production may be such that returns to scale may vary over dif­ferent ranges of output. Over some range we may have constant returns to scale, while over another range we may have increasing or decreasing returns to scale. In figure 3.21 we see that up to the level of output 4X returns to scale are constant; beyond that level of output returns to scale are decreasing. Production functions with varying returns to scale are difficult to handle and economists usually ignore them for the analysis of production.

With a non-homogeneous production function returns to scale may be increasing, constant or decreasing, but their measurement and graphical presentation is not as straightforward as in the case of the homogeneous production function. The isoclines will be curves over the production surface and along each one of them the K/L ratio varies.

In most empirical studies of the laws of returns homogeneity is assumed in order to simplify the statistical work. Homogeneity, however, is a special assumption, in some cases a very restrictive one. When the technology shows increasing or decreasing returns to scale it may or may not imply a homogeneous production function.

Causes of increasing returns to scale:

The increasing returns to scale are due to technical and/or managerial indivisibilities. Usually most processes can be duplicated, but it may not be possible to halve them. One of the basic characteristics of advanced industrial technology is the existence of ‘mass-production’ methods over large sections of manufacturing industry. ‘Mass- production’ methods (like the assembly line in the motor-car industry) are processes available only when the level of output is large. They are more efficient than the best available processes for producing small levels of output.

For example, assume that we have three processes:

The K/L ratio is the same for all processes and each process can be duplicated (but not halved). Each process has a different ‘unit’-level. The larger-scale processes are technically more productive than the smaller-scale processes. Clearly if the larger-scale processes were equally productive as the smaller-scale methods, no firm would use them: the firm would prefer to duplicate the smaller scale already used, with which it is already familiar. Although each process shows, taken by itself, constant returns to scale, the indivisibilities will tend to lead to increasing returns to scale.

For X < 50 the small-scale process would be used, and we would have constant returns to scale. For 50 < X < 100 the medium-scale process would be used. The switch from the smaller scale to the medium-scale process gives a discontinuous increase in output (from 49 tons produced with 49 units of L and 49 units of K, to 100 tons produced with 50 men and 50 machines). If the demand in the market required only 80 tons, the firm would still use the medium-scale process, producing 100 units of X, selling 80 units, and throwing away 20 units (assuming zero disposal costs).

This is one of the cases in which a process might be used inefficiently, because this process operated inefficiently is still relatively efficient compared with the small-scale process. Similarly, the switch from the medium-scale to the large-scale process gives a discontinuous increase in output from 99 tons (produced with 99 men and 99 machines) to 400 tons (produced with 100 men and 100 machines).

If the demand absorbs only 350 tons, the firm would use the large-scale process inefficiently (producing only 350 units, or pro­ducing 400 units and throwing away the 50 units). This is because the large-scale process, even though inefficiently used, is still more productive (relatively efficient) compared with the medium-scale process.

Causes of decreasing returns to scale:

The most common causes are ‘diminishing returns to management’. The ‘management’ is responsible for the co-ordination of the activities of the various sections of the firm. Even when authority is delegated to individual managers (production manager, sales manager, etc.) the final decisions have to be taken from the final ‘centre of top management’ (Board of Directors).

As the output grows, top management becomes eventually overburdened and hence less efficient in its role as coordinator and ultimate decision-maker. Although advances in management science have developed ‘plateaux’ of management techniques, it is still a commonly observed fact that as firms grows beyond the appropriate optimal ‘plateaux’, management diseconomies creep in.

Another cause for decreasing returns may be found in the exhaustible natural re­sources: doubling the fishing fleet may not lead to a doubling of the catch of fish; or doubling the plant in mining or on an oil-extraction field may not lead to a doubling of output.

B. The Law of Variable Proportions: Short-Run Analysis of Production:

If one factor is variable while the other(s) is kept constant, the product line will be a straight line parallel to the axis of the variable factor .

In general if one of the factors of production (usually capital K) is fixed, the marginal product of the variable factor (labour) will diminish after a certain range of production. We said that the traditional theory of production concentrates on the ranges of output over which the marginal products of the factors are positive but diminishing. The ranges of increasing returns (to a factor) and the range of negative productivity are not equi­librium ranges of output.

If the production function is homogeneous with constant or decreasing returns to scale everywhere on the production surface, the productivity of the variable factor will necessarily be diminishing. If, however, the production function exhibits increasing returns to scale, the diminishing returns arising from the decreasing marginal product of the variable factor (labour) may be offset, if the returns to scale are considerable. This, however, is rare. In general the productivity of a single-variable factor (ceteris paribus) is diminishing.

Let us examine the law of variable proportions or the law of diminishing productivity (returns) in some detail.

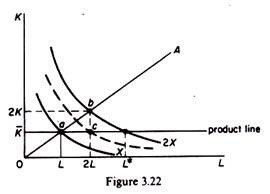
If the production function is homogeneous with constant returns to scale everywhere, the returns to a single-variable factor will be diminishing. This is implied by the negative slope and the convexity of the isoquants. With constant returns to scale everywhere on the production surface, doubling both factors (2K, 2L) leads to a doubling of output.

In figure 3.22 point b on the isocline 0A lies on the isoquant 2X. However, if we keep K constant (at the level K) and we double only the amount of L, we reach point c, which clearly lies on a lower isoquant than 2X. If we wanted to double output with the initial capital K, we would require L units of labour. Clearly L > 2L. Hence doubling L, with K constant, less than doubles output. The variable factor L exhibits diminishing productivity (diminishing returns).

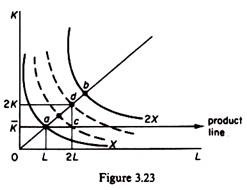
If the production function is homogeneous with decreasing returns to scale, the returns to a single-variable factor will be, a fortiori, diminishing. Since returns to scale are decreasing, doubling both factors will less than double output. In figure 3.23 we see that with 2L and 2K output reaches the level d which is on a lower isoquant than 2X. If we double only labour while keeping capital constant, output reaches the level c, which lies on a still lower isoquant.

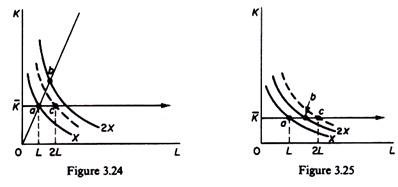
If the production function shows increasing returns to scale, the returns to the single- variable factor L will in general be diminishing (figure 3.24), unless the positive returns to scale are so strong as to offset the diminishing marginal productivity of the single- variable factor. Figure 3.25 shows the rare case of strong returns to scale which offset the diminishing productivity of L.