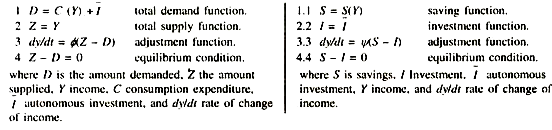Read this article to learn about the relation between effective demand and general equilibrium of an investment.
Thus, as a first approximation ‘effective demand’ might be thought of in terms of the schedule of ‘the sum of expected consumption and the expected investment.
The relation of ‘effective demand’ and general equilibrium can be shown by following equations:
Since we know that Y ≡ C + S, we can substitute this relation into Equation (2) to get Z = C + S. Subtracting Equation (I) from this latter relation, we get Z – D = S – I. Thus, general equilibrium can be explained in terms of consumption and investment or in terms of saving and investment. On the basis of above, we see that ex-ante saving can diverge from ex-post saving, which must equal the ex-post investment, which in turn can diverge from ex-ante investment.
ADVERTISEMENTS:
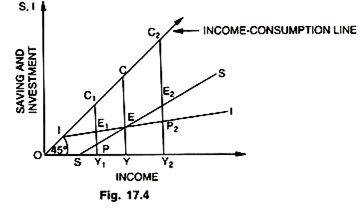
All the four will be equal only if all expectations are consistent with all plans; then expected incomes will equal actual incomes and expected sales will equal actual sales. One can call this general equilibrium. However, it is so only in a very special sense, for it is clearly possible that if plans and expectations change together in a perfectly consistent way, incomes and sales could be continuously changing yet always in equilibrium. This general equilibrium also called Y = C + I versus S = I approach is shown in the Fig. 17.4.
This functional equality of S and I alternatively is defined with reference to the equilibrium level of national income (Y = C + I) in the Keynesian system. The equilibrium level of national income (Y = C + I) is defined by the point of intersection of the aggregate demand function and the aggregate supply function called the point of effective demand. Thus, S = I is the same thing as Y = C + I. These are the two approaches which we have explained as the ‘backdoor’ and ‘front door’ approaches.
1. In this diagram OY is the unique equilibrium level of income, where saving EY is equal to investment EY and further Y = C + I, i.e., OY = CE (consumption) + EY (investment). Therefore S = I is the same thing as Y = C + I.
2. The economy is in disequilibrium at OY1, because investment (E1Y1) is greater than saving (PY1) or further at OY2 because savings E2Y2 exceed investment P1Y2. In the former case, the income must rise from OY1 to OY and in latter case it must fall from OY2 to OY, so that Y-C + l and S = I. Thus, we find that Keynesian functional equality of saving and investment enables us to understand the behaviour of the economy, the process of adjustment. It sheds light on the causal factors behind the equality of S and I. But it would be a mistake to imagine that an economist can be made out of a parrot, simply by teaching him the magic words saving and investment.
Behind these S and I schedules, lot of forces are at work. For example, the rate of interest may go up leading to a decline in the investment schedule; there may the an increase in public holdings of bonds, securities, etc., leading to a rise in consumption. The importance of all these factors and the forces behind these schedules is by no means to be ignored.