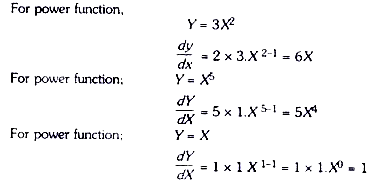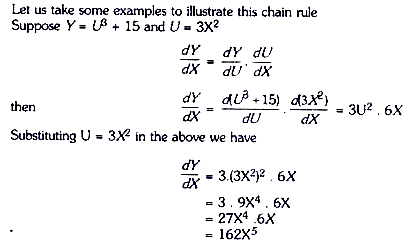Differentiation Calculus: Concept and Rules of Differentiation | Optimisation Technique

Optimisation techniques are an important set of tools required for efficiently managing firm’s resources.

In what follows we will focus on the use of differential calculus to solve certain types of optimisation problems.

Differential Calculus: The Concept of a Derivative:

In explaining the slope of a continuous and smooth non-linear curve when a change in the independent variable, that is, AX gets smaller and approaches zero, ∆Y /∆X becomes better approximation of the slope the function, Y = f (X), at a particular point. Thus, if ∆X is infinitesimally small, ∆Y /∆X measures the slope of the function at a particular point and is called the derivative of the function with respect to X. The derivative dY /dX or more precisely the first derivative of a function is defined as limit of the ratio ∆Y /∆X as ∆X approaches zero. Thus

dY/dX = limit ∆X→0 ∆Y/∆X

It is thus evident that derivative of a function shows the change in value of the dependent variable when change in the independent variable (∆X) becomes infinitesimally small. Note that derivative of a function [Y=f (X)] is also written as d (fX) / dX. Or f’ (X).

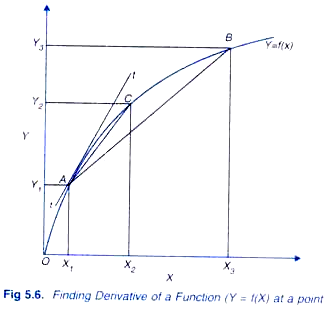
As explained above, the derivatively of a function at a point measures the slope of the tangent at that point. Consider Figure 5.6 when ∆X= X₃ – X₁, the slope of the corresponding straight line AB is equal to Y₃-Y₁/ X₃-X₁ becomes smaller and is equal to X₂-X_1, slope of that corresponding line AC is equal Y₂-Y₁/ X₂-X₁ .

It will be seen from Figure 5.6 that slope of line AC is more near to the slope of the tangent tt drawn at point A to the function curve. Similarly, if ∆X is reduced further, slope of the straight line between the two corresponding points will go on becoming closer and closer to the slope of the tangent tt drawn at point A to the curve. At the limit of ∆Y/ ∆X when ∆X approaches zero, slope of the tangent such as tt at a point on a function becomes the derivative dY/dX of the function with respect to X.

Thus, derivative dY/dX is slope of a function whether it is linear or non-linear and represents a change in the dependent variable due to a small change in the independent variable. The concept of a derivative is extensively used in economics and managerial decision making, especially in solving the problems of optimisation such as those of profit maximisation, cost minimisation, output and revenue maximisation. There are various types of functions and for them there are different rules for finding the derivatives. We will explain below the basic rules of finding derivatives of the various types of functions.

Rules of Differentiation:

Process of finding the derivative of a function is called differentiation. As stated above, derivative of a function represents the change in the dependent variable due to a infinitesimally small change in the independent variable and is written as dY / dX for a function Y = f (X). A series of rules have been derived for differentiating various types of functions. We describe below these rules of differentiation.

Derivative of a Constant Function:

A constant function is expressed as

Y=f(X) = a

Where ‘a’ is constant. The constant ‘a’ implies that Y does not vary as X varies, that is. Y is independent of X. Therefore, the derivative of a constant function is equal to zero. Thus, in this constant function

dy/dx = 0

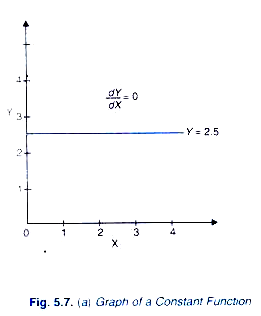
For example, let the constant function be Y = 2.5

This is graphed in Figure 5.7(a). It will be seen that a constant function is a horizontal straight line (having a zero slope) which shows that irrespective of the value of the variable X, the value of Y does not change at all. Therefore, derivative dY/dX = 0.

Derivative of a Power Function:

A power function takes the following form:

Y = aX^b

Where a and b are constants. Here a is the coefficient of the X term and the variable X is raised to the power b. The derivative of this power function is equal to the power b multiplied by the coefficient a times the variable X raised to the power b – 1. Thus rule for the derivative of power function (Y = a X^b) is

dY / dX = b. a. Xb^-1

Let us take some examples of determining the derivative of a power function.

First, take the following power function:

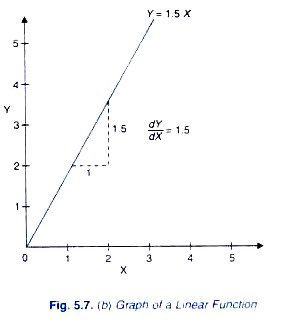
Y = 1.5 X

In this function 1.5 is the coefficient of variable X, that is, a and the power b of X is 1 (implicit). Using the above rule for the derivative of a power function we have

dY / dX = 1 X 1.5 X^1-1 = 1 X 1.5 X 0 = 1.5 X⁰ = 1.5

This is graphically shown in Figure 5.7(b). It will be seen from this figure that slope of the linear function (Y = 1.5 X) is constant and is equal to 1.5 over any range of the values of the variables X.

Quadratic Power Function:

Let us take the following example of a power function which is of quadratic type:

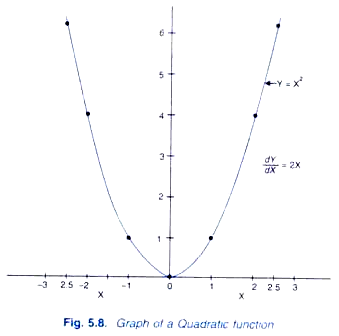
Y=X²

Its derivative, dy/ dx =2X^2-1 = 2X¹ = 2X

To illustrate it we have calculated the values of Y, associated with different values of X such as 1, 2, 2.5 and -1, -2, -2.5 and have been shown in Table 5.3.

We have plotted the values of X and corresponding values of Y to get a U-shaped parabolic curve in Figure 5.8. It will be seen that derivative dY / dX or, in other words, slope of this quadratic function is changing at different values of X.

Some other examples of power function and their derivatives are:

It should be noted that any variable raised to the zero power (as in our example X⁰) is equal to 1

For power function,

Y = 3X^-2

dY / dX = -2 x 3.X^-2-1 = -6X^-3

Derivative of a Sum or Difference of Two Functions:

The derivative of a sum of the two functions is equal to the sum of the derivatives obtained separately of the two functions.

Derivative of a Product of the Two Functions:

Suppose Vis the product of the two separate functions f (X) and g(X).

Y=f (X). g (X)

The derivative of the product of these two functions is equal to the first function multiplied by the derivative of the second function plus the second function multiplied by the derivative of the first function. Thus,

Derivative of the Quotient of the Two Functions:

Suppose the variable 7is equal to the quotient of the two functions f (X) and g(X). That is,

Y =f (X) / g(X)

Derivative of Function of a Function (Chain Rule):

When a variable Y is function of a variable U which in turn is related to another variable X, and if we wish to obtain a derivative of Y with respect to X, then we use chain rule for this purpose. Suppose variable Vis a function of the variable U, that is, Y = f (U) and variable U is a function of variable X, that is, U = g (X). Then, to obtain the derivative of Y with respect to X, that is dY / dX, we first find the derivative of the two functions, Y = f(U) and U = g(X) separately and then multiply them together. Thus,

Thus, according to the chain rule if Y= f(U) and U = g(X), then derivative of Y with respect X, can be obtained by multiplying together the derivative of Y with respect to U and the derivative of U with respect to X

Let us take some examples to illustrate this chain rule

Suppose Y = U³ + 15 and a = 3X²