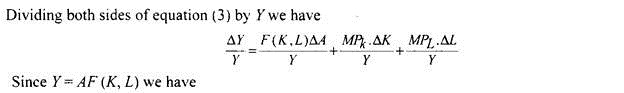Solow’s Neoclassical Growth Model | Economic Growth | Economics

Robert Solow and Denison have attempted to study the relative importance of the various sources of economic growth by using the concept of production function. The rate of economic growth in an economy and differences in income levels of different countries and also their growth performance during a period can be explained in terms of the increase in these sources of economic growth.

An important issue in growth economics is what contributions of different factors, namely, capital, labour and technology make to economic growth? In other words, what is the relative importance of these different factors as sources of economic growth.

It will be recalled that the production function describes that the amount of total output produced depends on the amount of different factors used and the state of technology.

The following production function has been used to measure the various sources of economic growth:

Y=AF (K,L) …(1)

Where, Y= total national product

K = the quantity of physical capital used

L = the quantity of labour used

A = the state of technology

The production function equation (1) shows that increase in capital and labour and improvement in technology will lead to growth in national output.

Growth Accounting and Total Factor Productivity:

Note that improvement in technology causes output increases with the given factor supplies. In other words, advancement in technology leads to the increase in productivity of factors used. There­fore, improvement in technology is generally measured by growth in total factor productivity (TFP).

It will also be noticed from the production function equation (1) that technology (A) has been taken to be a multiplicative factor. This implies that progress in technology increases the marginal productivity of both capital and labour uniformly. Such technological change is generally referred to as neutral technological change. Besides, we measure the sources of economic growth with the above production function by assuming constant returns to scale. Constant returns to scale implies that increase in inputs, that is, labour and capital, by a given percentage will lead to the same percentage increase in output. Further, the increase in improvement in technology (A) or what is also referred to as increase in total factor productivity causes a shift in the production function.

With the above assumptions it can be proved that the following factors represent the sources of economic growth:

Or Growth of Output = (Share of Capital x Growth in Capital) + (Share of Labour x Growth in Labour) + Technical Progress (or Growth in Total Factor Productivity)

Where, θ denotes share of capital in national product, 1-θ share of labour in national product.

The above equation, which is generally referred to as growth accounting equation, shows the various sources of growth which are summarized below:

1. The contribution of increase in capital to the growth in output (G or ∆Y/Y) is given by increase in (∆K/K) capital multiplied by the share (θ) of capital in national product;

2. The increase in labour force contributes to rate of economic growth equal to the labour share (1 – θ) in national product multiplied by the growth in labour force (∆L/L); and

3. The technological improvement ∆ A/A which is measured by the increase in total factor productivity also makes an important contribution to economic growth. Technological progress leads to the increase in total factor productivity (TFP) which implies that with the given resources (i.e. capital and labour) more output can be produced.

Proof:

We can formally prove the growth accounting equation explained above. In the production function equation (1) the change in output (∆Y) depends on changes in various inputs or factors capital and labour ∆K and ∆L and change in technology. This can be written as under–

∆Y=F (KL) ∆A +MP_k x ∆K + MP_L x ∆L … (3)

Where, MP_k and MP_L represent marginal products of labour and capital respectively.

The above is the same as growth accounting equation (2) which indicates the sources of growth of output.

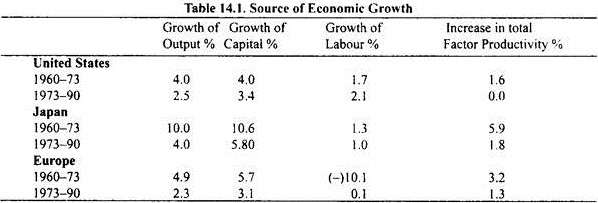
In Table 14.1 we present the contributions made by capital, labour and total factor productivity (i.e., technical improvement) in growth of output in the United States, Japan and the major countries of Europe in the two periods 1960-73 and 1973-90. It will be seen from the table that growth of capital and improvement in total factor productivity (i.e., technological progress) have been the important sources of economic growth, especially in case of economic growth in Japan and European countries.

Table 14.1 further reveals that it is decline in total factor productivity (i.e. technological improvement) and in growth of capital that is responsible for slowdown of economic growth in the USA, Japan and European countries during the period 1973-90.

Limitations of Solow’s Neoclassical Growth Model:

1. Knowledge or Education is the Missing Factor:

In the above growth accounting equation one factor, namely, knowledge or education, is missing which has been stressed among others by Nobel Laureate Prof. Amartya Sen as an important factor contributing to economic growth. It may be noted that increase in knowledge or education increases the productivity of workers by improving their productive skills and abilities.

Besides, increased knowledge raises the productivity of capital and raises the return to investment in capital goods. Since investment in promotion of knowledge or education makes workers and machine more productive, the workforce equipped with knowledge and education is often called human capital which is regarded by modern economists as an important source of economic growth. Thus human capital or knowledge and education are the important missing factor in the growth equation of neoclassical economists, Solow and Denison. On including human capital as a separate factor which contributes to growth of output, the production function can be written as under–

Y = AF (K,L,H)

Where, H represents human capital which was omitted by Robert Solow in his growth accounting equation.

2. Ignores Economies of Scale as a Factor Contributing to Growth:

Robert Solow in his study of sources of growth in real income also did not consider economies of scale as a factor contributing to growth. Solow assumed constraint returns to scale which implies if each factor in the production function increases by one per cent, output also increases by one per cent. However, some economists such as Denison and those associated with World Bank emphasise economies of scale or what is also called increasing returns to scale as a separate factor determining the rate of economic growth.

In case of the United States Denison estimated that of 2.92 per cent annual growth in national income recorded during the period 1929-1982, 0.26 per cent was due to economies of scale. However, whether there are increasing returns to scale or constant returns to scale is an empirical matter for investigation.

Key Results of Solow’s Neoclassical Model:

Various key results of Solow’s neoclassical growth model are as follows:

1. Neoclassical growth theory explains that output is a function of growth in factor inputs, especially capital and labour, and technological progress.

2. Contribution of increase in labour to the growth in output is the most important.

3. Growth rate of output in steady-state equilibrium is equal to the growth rate of population or labour force and is exogenous of the saving rate, that is, it does not depend upon the rate of saving.

4. Although saving rate does not determine the steady-state growth rate in output, it does cause an increase in steady-state level of per capita income (and therefore also total income) through raising capital per head.

5. Steady-state rate of growth of per capita income, that is, long-run growth rate is determined by progress in technology.

6. If there is no technical progress, then output per capita will ultimately converge to steady- state level.

7. A significant conclusion of neoclassical growth theory is that if the two countries have the same rate of saving and same rate of population growth and have access to the same technology (i.e. production function), their levels of per capita income will eventually converge, that is, they will ultimately become equal. In this context it is worthwhile to quote Dornbusch, Fischer and Startz. The poor countries are poor because they have a less capital but if they save at the same rate as rich countries, and have access to the same- technology, they will eventually catch up.